题目内容
函数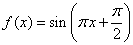 ,
,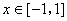 ,则
,则
A.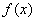 为偶函数,且在 为偶函数,且在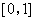 上单调递减 上单调递减 |
B.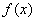 为偶函数,且在 为偶函数,且在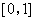 上单调递增 上单调递增 |
C.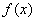 为奇函数,且在 为奇函数,且在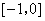 上单调递增 上单调递增 |
D.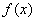 为奇函数,且在 为奇函数,且在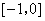 上单调递减 上单调递减 |
A
解析试题分析: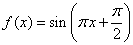

 ,易知
,易知 ,所以
,所以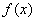 是偶函数.
是偶函数.
又因为 时,
时, ,所以
,所以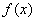 在
在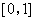 上单调递减.
上单调递减.
考点:三角函数的单调性、奇偶性
点评:本题解题的关键是先利用诱导公式化简,之后再利用判断函数单调性,奇偶性的一般
方法进行判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 是定义在
是定义在 上的偶函数,且对任意
上的偶函数,且对任意 ,都有
,都有 ,当
,当
 时,
时, ,则函数
,则函数 在区间
在区间 上的反函数
上的反函数 的值
的值 ( )
( )
A. | B. | C.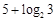 | D. |
如图是函数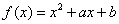 的部分图象,则函数
的部分图象,则函数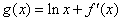 的零点所在的区间是( )
的零点所在的区间是( )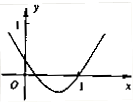
A. | B.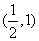 | C.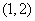 | D. |
如图是函数 的大致图象,则
的大致图象,则 等于( )
等于( )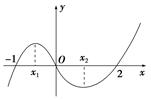
| A.1 | B.0 | C. | D. |
函数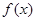 对任意自然数
对任意自然数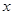 ,满足
,满足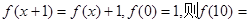 ( )
( )
| A.11 | B.12 | C.13 | D.14 |
下列四组函数,表示同一函数的是( )
A. |
B. |
C. |
D. |
函数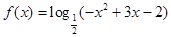 的单调递减区间为
的单调递减区间为
A.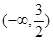 | B.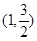 | C.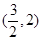 | D. |
已知 是函数
是函数 的零点,若
的零点,若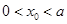 ,则
,则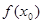 的值满足( )
的值满足( )
A.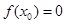 | B.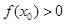 |
C.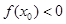 | D.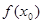 的符号不确定 的符号不确定 |
 在定义域内可导,
在定义域内可导,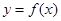 的图象如下左图所示,则导函数
的图象如下左图所示,则导函数 的图象可能是( )
的图象可能是( )