题目内容
设函数 ,给出下列命题:
,给出下列命题:
(1) 有最小值;
有最小值;
(2)当 时,
时, 的值域为
的值域为 ;
;
(3)当 时,
时, 在区间
在区间 上有单调性;
上有单调性;
(4)若 在区间
在区间 上单调递增,则实数a的取值范围是
上单调递增,则实数a的取值范围是 .
.
则其中正确的命题是 .
②③
解析试题分析: 的最小值为
的最小值为 ,所以函数
,所以函数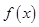 无最小值,(1)错误;当
无最小值,(1)错误;当 时
时
 可取到所有的正数,所以函数值域为R,(2)正确;当
可取到所有的正数,所以函数值域为R,(2)正确;当 时
时 的对称轴
的对称轴 ,在
,在 上是增函数,所以函数
上是增函数,所以函数 在
在 上是增函数,(3)正确;若
上是增函数,(3)正确;若 在区间
在区间 上单调递增,所以
上单调递增,所以 在
在 上递增且函数值
上递增且函数值
 (3)错误
(3)错误
考点:复合函数单调性
点评:复合函数单调性由构成它的两基本初等函数单调性决定,两基本初等函数单调性相同则复合后递增,单调性相反则复合后递减

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 ”,命题q:“存在
”,命题q:“存在 ”若命题“p且q”是真命题,则实数
”若命题“p且q”是真命题,则实数 的取值范围是___________.
的取值范围是___________.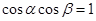 ,则
,则 ;
; 与函数
与函数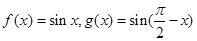 的图像分别交于点
的图像分别交于点 ,则
,则 的最大值为
的最大值为 ;
; 为单调递增数列,则
为单调递增数列,则 取值范围是
取值范围是 ;
; 的通项
的通项 ,前
,前 项和为
项和为 ,则使
,则使 的
的 ∈R,
∈R, +2
+2 +2≤0的否定;
+2≤0的否定; +x-m=0有实根的逆命题;
+x-m=0有实根的逆命题; x的双曲线的离心率为
x的双曲线的离心率为 ;
; 中,当解释变量
中,当解释变量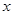 每增加1个单位时,则预报变量
每增加1个单位时,则预报变量 减少0.4个单位; ④对分类变量X与Y来说,它们的随机变量
减少0.4个单位; ④对分类变量X与Y来说,它们的随机变量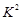 的观测值
的观测值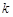 越小,“X与Y有关系”的把握程度越大; ⑤在回归分析模型中,残差平方和越小,说明模型的拟合效果越好.
越小,“X与Y有关系”的把握程度越大; ⑤在回归分析模型中,残差平方和越小,说明模型的拟合效果越好.
 ,那么
,那么 的 条件(“充要”,“充分不必要”,“必要不充分” “既不充分又不必要”)
的 条件(“充要”,“充分不必要”,“必要不充分” “既不充分又不必要”) ”的否定是 .
”的否定是 . ,则
,则 ”的逆否命题为________________
”的逆否命题为________________