题目内容
函数
的图象关于（ ）A．原点对称，在（0，+∞）为增函数
B．y轴对称，在（0，+∞）为增函数
C．原点对称，在（0，+∞）为减函数
D．y轴对称，在（0，+∞）为减函数
【答案】分析：由选项知，只需判断函数f（x）的奇偶性、单调性即可得到答案．
解答：解：函数f（x）的定义域为{x|x≠0}，关于原点对称．
又f（-x）=-x+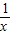
=-（x-
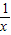）=-f（x），
所以f（x）为奇函数，
故其图象关于原点对称；
当x∈（0，+∞）时，x单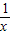调递增，-
单调递增，
所以f（x）=x-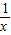
单调递增；
综上，知f（x）的图象关于原点对称，且在（0，+∞）上为增函数，
故选A．
点评：本题考查函数的奇偶性、单调性及奇函数图象的对称性，属基础题．
解答：解：函数f（x）的定义域为{x|x≠0}，关于原点对称．
又f（-x）=-x+
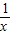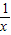=-（x-）=-f（x），所以f（x）为奇函数，
故其图象关于原点对称；
当x∈（0，+∞）时，x单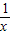调递增，-
单调递增，所以f（x）=x-
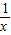单调递增；综上，知f（x）的图象关于原点对称，且在（0，+∞）上为增函数，
故选A．
点评：本题考查函数的奇偶性、单调性及奇函数图象的对称性，属基础题．
练习册系列答案
相关题目
