Question

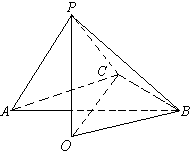
已知等腰DABC中，AC = BC = 2，ACB = 120°，DABC所在平面外的一点P到三角形三顶点的距离都等于4，求直线PC与平面ABC所成的角。

Answer 1

解析:

解：设点P在底面上的射影为O，连OB、OC，

                            则OC是PC在平面ABC内的射影，

                            ∴PCO是PC与面ABC所成的角。

                            ∵ PA = PB = PC，

                            ∴点P在底面的射影是DABC的外心，

                            注意到DABC为钝角三角形，

                            ∴点O在DABC的外部，

                            ∵AC = BC，O是DABC的外心，

                            ∴OC⊥AB                

                            在DOBC中，OC = OB， OCB = 60°，

                            ∴DOBC为等边三角形，∴OC = 2                

                            在RtDPOC中，

                            ∴PCO = 60° 。