题目内容
已知复数z1=a+bi,z2=c+di(a,b,c,d∈R).
(1)在复平面中,若OZ1⊥OZ2(O为坐标原点,复数z1,z2分别对应点Z1,Z2),求a,b,c,d满足的关系式;
(2)若|z1|=|z2|=1,|z1-z2|= ,求|z1+z2|.
,求|z1+z2|.
解:(1)由OZ1⊥OZ2 ,得 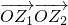 =0,即 ac+bd=0.----------6分
=0,即 ac+bd=0.----------6分
(2)∵(z1-z2 )( )=
)=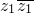 +
+ -(
-( +
+ )=|z1-z2|2=3,
)=|z1-z2|2=3,
即 1+1-( +
+ )=3,∴(
)=3,∴( +
+ )=-1,--------10分
)=-1,--------10分
∴|z1+z2|2=(z1+z2 )( )=
)=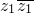 +
+ +(
+( +
+ )=1+1-1=1.
)=1+1-1=1.
故|z1+z2|=1.------14分.
分析:(1)由OZ1⊥OZ2 ,得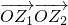 =0,即 ac+bd=0.
=0,即 ac+bd=0.
(2))根据(z1-z2 )( )=
)=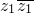 +
+ -(
-( +
+ )=3,求出(
)=3,求出( +
+ )=-1,再由
)=-1,再由
|z1+z2|2=(z1+z2 )( )=
)=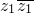 +
+ +(
+( +
+ )=1求出|z1+z2|的值.
)=1求出|z1+z2|的值.
点评:本题主要考查复数的代数形式的表示法及其几何意义,求复数的模,利用了 .
.
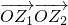 =0,即 ac+bd=0.----------6分
=0,即 ac+bd=0.----------6分(2)∵(z1-z2 )(
 )=
)=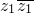 +
+ -(
-( +
+ )=|z1-z2|2=3,
)=|z1-z2|2=3,即 1+1-(
 +
+ )=3,∴(
)=3,∴( +
+ )=-1,--------10分
)=-1,--------10分∴|z1+z2|2=(z1+z2 )(
 )=
)=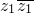 +
+ +(
+( +
+ )=1+1-1=1.
)=1+1-1=1.故|z1+z2|=1.------14分.
分析:(1)由OZ1⊥OZ2 ,得
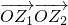 =0,即 ac+bd=0.
=0,即 ac+bd=0.(2))根据(z1-z2 )(
 )=
)=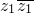 +
+ -(
-( +
+ )=3,求出(
)=3,求出( +
+ )=-1,再由
)=-1,再由|z1+z2|2=(z1+z2 )(
 )=
)=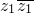 +
+ +(
+( +
+ )=1求出|z1+z2|的值.
)=1求出|z1+z2|的值.点评:本题主要考查复数的代数形式的表示法及其几何意义,求复数的模,利用了
 .
. 
练习册系列答案
相关题目