题目内容
已知在△ABC中, a、b、c分别为角A、B、C的对边,且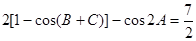
(1)若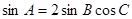 ,试判断△ABC的形状;
,试判断△ABC的形状;
(2)若a=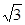 ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
(1)△ABC是等边三角形(2)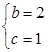 或
或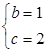
解析试题分析:(1)∵cos(B+C)=-cosA, 2分 由2[1-cos(B+C)]-(2cos2A-1)=
由2[1-cos(B+C)]-(2cos2A-1)=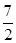 得
得
∴4cos2A-4cosA+1=0, 4分
∴(2cosA-1)2=0,即cosA=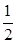 . 6分
. 6分 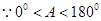 ∴A=60° 7分
∴A=60° 7分
∵ 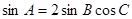 ∴
∴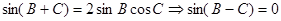
∴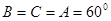 ,故△ABC是等边三角形 10分
,故△ABC是等边三角形 10分
(2)∵a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc, 13分
∵a=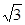 ,b+c=3,∴3=9-3bc,∴bc=2,
,b+c=3,∴3=9-3bc,∴bc=2,
由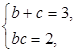 解之得
解之得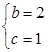 或
或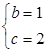 . 15分
. 15分
考点:三角函数诱导公式及余弦定理解三角形
点评:第一问主要是应用三角函数公式化简出三内角大小关系从而确定三角形形状;第二问借助于余弦定理找到边角间的关系式,从而解出边长

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目