Question

已知函数f(x)=|x²-4x+3|.

(1)求函数f(x)的单调区间,并指出增减性;

(2)求集合M={m|使方程f(x)=mx有四个不相等的实根}.?

Answer 1

解析: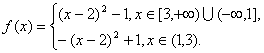

(1)递增区间为［1,2］,［3,+∞),?

递减区间为(-∞,1］,［2,3).?

(2)?

?

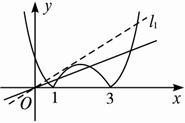
由图象可知y=f(x)与y=mx图象有四个不同的交点,直线y=mx应介于x轴与切线l₁之间.?

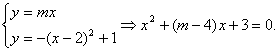
Δ=0得m=4±2.

m=4+2时,x=-(1,3)舍去.?

∴m=4-2,l₁方程为y=(4-2)x.?

∴m∈(0,4-2).