题目内容

设变量x，y满足约束条件
x-y≥-1
x+y≤6
y≥2
，则目标函数z=xy的取值范围为（　　）
A、[2，8]
B、[2，
35
4
]
C、[2，9]
D、[8，
35
4
]
分析：根据已知的约束条件
x-y≥-1
x+y≤6
y≥2
，画出满足约束条件的可行域，分析目标函数z=xy表示的几何意义，结合图象即可给出z的取值范围．
解答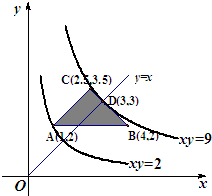：精英家教网解：如图，可行域为△ABC的边界及内部，
双曲线xy=z与可行域有公共点时，
2≤z≤9．
故选C．
点评：平面区域的范围问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，分析表达式的几何意义，然后结合数形结合的思想，分析图形，找出满足条件的点的坐标，即可求出答案．
练习册系列答案
相关题目
设变量x，y满足约束条件
y≤2
3
x-3y≤0
x+
3
y-2
3
≥0
，则目标函数u=x2+y2的最大值M与最小值N的比
M
N
=（　　）
A、
4
3
3
B、
16
3
3
C、
4
3
D、
16
3
设变量x，y满足约束条件
x+y≥2
x≤1
y≤2
，则目标函数z=-x+y的最大值是（　　）
（2013•河西区一模）设变量x、y满足约束条件
y≥0
x-y+1≥0
x+y-3≤0
，则z=2x+y的最大值为
6
6
．
（理科）设变量x，y满足约束条件
2x-y≤0
x-3y+5≥0
x≥0
，则目标函数z=x-y的最大值为（　　）
（2012•江西模拟）设变量x，y满足约束条件
x+1≥0
x-y+1≤0
x+y-2≤0
，则z=4x+y的最大值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网