题目内容
设P，Q两个非空集合，定义运算“⊙”；P⊙Q={ x|x∈P∪Q，且x∉P∩Q}，如果P={ y|y=
}，Q={ y|y=2x，x＞0 }，则P⊙Q=（ ）
| 4-x2 |
分析：先求出集合P，Q的等价条件，然后利用定义求P⊙Q即可．
解答：解：∵0≤
≤2，
∴P={y|0≤y≤2}．
∵Q={ y|y=2x，x＞0 }={ y|y＞1}．
∴P∪Q={y|0≤y≤2}∪{ y|y＞1}={ y|y≥0}．
P∩Q={y|0≤y≤2}∩{ y|y＞1}={ y|1＜y≤2}．
∴P⊙Q={ x|x∈P∪Q，且x∉P∩Q}={y|0≤y≤1或y＞2}．
即P⊙Q=[0，1]∪（2，+∞）．
故选：A．
| 4-x2 |
∴P={y|0≤y≤2}．
∵Q={ y|y=2x，x＞0 }={ y|y＞1}．
∴P∪Q={y|0≤y≤2}∪{ y|y＞1}={ y|y≥0}．
P∩Q={y|0≤y≤2}∩{ y|y＞1}={ y|1＜y≤2}．
∴P⊙Q={ x|x∈P∪Q，且x∉P∩Q}={y|0≤y≤1或y＞2}．
即P⊙Q=[0，1]∪（2，+∞）．
故选：A．
点评：本题主要考查集合的基本运算，正确理解运算“⊙”是解决本题的关键．
练习册系列答案
相关题目
设P、Q是两个非空集合，定义集合间的一种运算“⊙”：P⊙Q={x|x∈P∪Q，且x∉P∩Q}．如果P={y|y=
}，Q={y|y=4x，x＞0}，则P⊙Q=（ ）
| 4-x2 |
| A、[0，1]∪（2，+∞） |
| B、[0，1]∪[4，+∞） |
| C、[1，4] |
| D、（4，+∞） |
设P、Q是两个非空集合，定义集合间的一种运算“⊙”：P⊙Q={x|∈P∪Q，且x∉P∩Q}如果P={x|y=
}，Q={y|y=4x，x＞0}，则P⊙Q=（ ）
| 4-x2 |
| A、[-2，1]∪（2，+∞） |
| B、[-2，1]∪[2，+∞） |
| C、[1，2] |
| D、（2，+∞） |
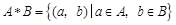，若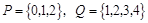
，则P*Q中元素的个数是（ ）