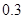题目内容
学校为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为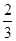 和
和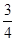 ,且各株大树是否成活互不影响.
,且各株大树是否成活互不影响.
(Ⅰ)求移栽的4株大树中恰有3株成活的概率;
(Ⅱ)设移栽的4株大树中成活的株数为 ,求
,求 分布列与期望.
分布列与期望.
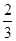 和
和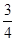 ,且各株大树是否成活互不影响.
,且各株大树是否成活互不影响.(Ⅰ)求移栽的4株大树中恰有3株成活的概率;
(Ⅱ)设移栽的4株大树中成活的株数为
 ,求
,求 分布列与期望.
分布列与期望.(I)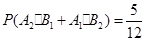
(II)综上知 有分布列:
有分布列:
从而, 的期望为
的期望为
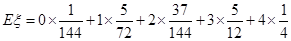
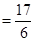 (株).
(株).
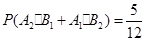
(II)综上知
 有分布列:
有分布列: | 0 | 1 | 2 | 3 | 4 |
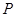 | 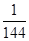 | 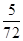 | 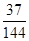 | 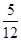 | 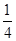 |
 的期望为
的期望为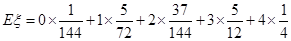
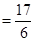 (株).
(株).本试题主要考查了独立事件的概率公式,以及二项分布的综合运用。
(1)中需要明确移栽的4株大树中恰有3株成活,分为几种情况来讨论,甲有一株成活,乙有两株成活;甲有两株成活,乙有一株成活; 分别讨论得到。
(2)根据已知条件可知 的所有可能值为0,1,2,3,4,然后利用独立事件的概率的乘法公式可到各个取值的概率值,表示分布列和期望值。
的所有可能值为0,1,2,3,4,然后利用独立事件的概率的乘法公式可到各个取值的概率值,表示分布列和期望值。
解:设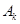 表示甲种大树成活
表示甲种大树成活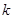 株,
株,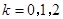 ,
,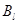 表示乙种大树成活
表示乙种大树成活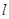 株,
株,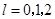 ,
,
则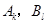 独立.由独立重复试验中事件发生的概率公式有
独立.由独立重复试验中事件发生的概率公式有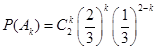 ,
,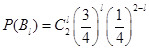 .据此算得
.据此算得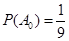 ,
,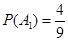 ,
,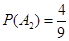 ,
,
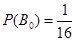 ,
,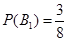 ,
, .
.
(I)所求概率为
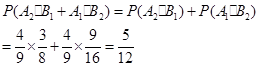
(II)解法一: 的所有可能值为0,1,2,3,4,且
的所有可能值为0,1,2,3,4,且
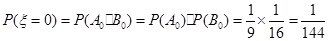 ,
,
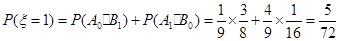 ,
,
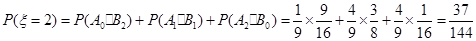 ,
,
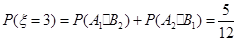 ,
,
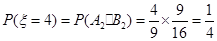 .
.
综上知 有分布列:
有分布列:
从而, 的期望为
的期望为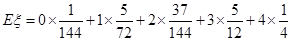
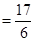 (株).
(株).
解法二:分布列的求法同前.令 ,
,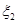 分别表示甲、乙两种树成活的株数,则
分别表示甲、乙两种树成活的株数,则
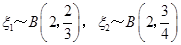 ,故有
,故有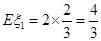 ,
,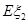 =
=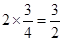 ,
,
从而知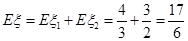 (株)
(株)
(1)中需要明确移栽的4株大树中恰有3株成活,分为几种情况来讨论,甲有一株成活,乙有两株成活;甲有两株成活,乙有一株成活; 分别讨论得到。
(2)根据已知条件可知
 的所有可能值为0,1,2,3,4,然后利用独立事件的概率的乘法公式可到各个取值的概率值,表示分布列和期望值。
的所有可能值为0,1,2,3,4,然后利用独立事件的概率的乘法公式可到各个取值的概率值,表示分布列和期望值。解:设
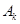 表示甲种大树成活
表示甲种大树成活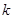 株,
株,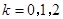 ,
,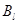 表示乙种大树成活
表示乙种大树成活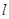 株,
株,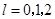 ,
,则
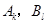 独立.由独立重复试验中事件发生的概率公式有
独立.由独立重复试验中事件发生的概率公式有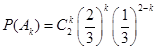 ,
,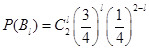 .据此算得
.据此算得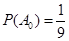 ,
,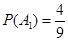 ,
,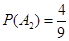 ,
,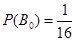 ,
,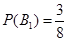 ,
, .
.(I)所求概率为
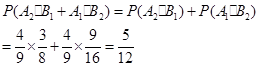
(II)解法一:
 的所有可能值为0,1,2,3,4,且
的所有可能值为0,1,2,3,4,且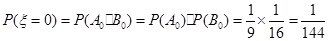 ,
,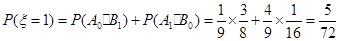 ,
,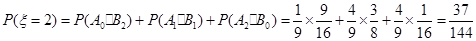 ,
,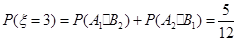 ,
,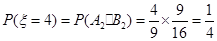 .
.综上知
 有分布列:
有分布列: | 0 | 1 | 2 | 3 | 4 |
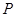 | 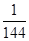 | 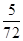 | 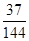 | 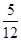 | 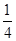 |
 的期望为
的期望为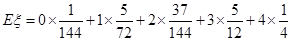
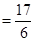 (株).
(株).解法二:分布列的求法同前.令
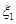 ,
,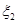 分别表示甲、乙两种树成活的株数,则
分别表示甲、乙两种树成活的株数,则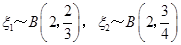 ,故有
,故有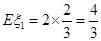 ,
,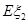 =
=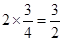 ,
,从而知
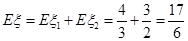 (株)
(株)
练习册系列答案
相关题目
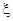 的概率分布率由下图给出:
的概率分布率由下图给出:


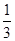
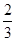 ,乙获胜的概率为
,乙获胜的概率为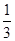 ,假定各次比赛相互独立,比赛经ξ次结束,求:
,假定各次比赛相互独立,比赛经ξ次结束,求: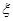 是离散型随机变量,
是离散型随机变量,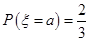 ,
,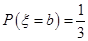 ,且a<b,又Eξ=
,且a<b,又Eξ=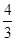 ,Dξ=
,Dξ=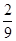 ,则a+b的值为( )
,则a+b的值为( )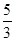


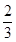 ,被乙小组攻克的概率为
,被乙小组攻克的概率为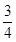 ,
,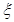 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求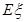 ;
;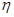 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数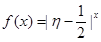 在定义域内单调递增”为事件C,求事件C发生的概率;
在定义域内单调递增”为事件C,求事件C发生的概率; 的分布列如下表所示,
的分布列如下表所示, ,则
,则 的值等于 ;
的值等于 ; 
 的分布如图所示则数学期望
的分布如图所示则数学期望 .
.