题目内容
(本题满分12分)
设 ,且
,且 满足
满足
(1)求 的值.
的值.
(2)求 的值.
的值.
(1)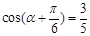 .(2)
.(2)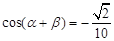 .
.
解析试题分析:(1)根据已知条件,将给出的方程组的每一个方程,利用化为单一函数的思想得到结论。
(2)经过第一问的求解,得到两个关系式一个是角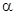 ,一个角
,一个角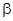 的三角函数式,然后整体构造所求解的角,结合两角和差的公式化简求值。
的三角函数式,然后整体构造所求解的角,结合两角和差的公式化简求值。
解:(1)∵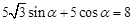 ,∴
,∴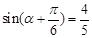 (3分)
(3分)
∵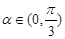 ,∴
,∴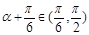 ,∴
,∴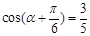 . (4分)
. (4分)
(2)又∵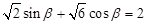 ,∴
,∴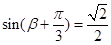 , (6分)
, (6分)
∵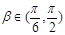 ,∴
,∴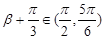 ,∴
,∴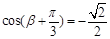 , (7分)
, (7分)
∴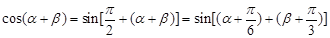
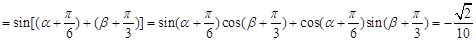
∴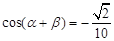 .
.
考点:本试题主要考查了两角和差的三角恒等变换的运用。
点评:解决该试题的关键是能够根据已知条件整体的思想来构造所求解的角,结合两角和差的公式来得到,主义同角公式的平方关系的使用,确定出角的范围,避免出现多解。

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
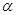 的终边经过点
的终边经过点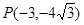 求
求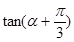 的值。
的值。 )=
)=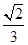 ,求tan2θ的值.
,求tan2θ的值.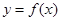
 .
.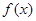 的最小正周期和最大值;
的最小正周期和最大值;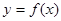 在区间
在区间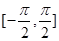 上的图象.
上的图象.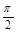 ,且方程
,且方程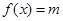 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围.
 化成
化成 的形式;
的形式; 的值;
的值; 始终为
始终为 (其中点P,Q分别在边BC,CD上),设
(其中点P,Q分别在边BC,CD上),设 .
.

 的周长l是否为定值;
的周长l是否为定值; ,
, ,设函数
,设函数
 的图象关于直线
的图象关于直线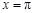 对称,其中
对称,其中 ,
, 为常数,且
为常数,且 .
.  的最小正周期;
的最小正周期; 的图象经过点
的图象经过点 ,求函数
,求函数 上的取值范围.
上的取值范围.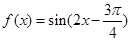 ,
,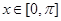
 的图像.
的图像.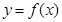 的图象是由
的图象是由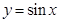 的图象经过怎样的变换得到的.
的图象经过怎样的变换得到的.
 ,求
,求 时函数
时函数 的最值。
的最值。