题目内容
已知正项数列{an}中,Sn是其前n项的和,且 ,n∈N+.
,n∈N+.
(Ⅰ)计算出a1,a2,a3,然后猜想数列{an}的通项公式;
(Ⅱ)用数学归纳法证明你的猜想.
解:(I)由于 ?
?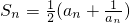
当n=1时, ,可得a1=1,
,可得a1=1,
当n=2时, ,可得
,可得 (an>0),
(an>0),
当n=3时,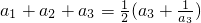 ,可得
,可得 (an>0),
(an>0),
猜想: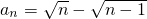 (n∈N+)
(n∈N+)
(II)证明:(1)当n=1时,已证.
(2)假设n=k(k≥1)时, 成立,则当n=k+1时,
成立,则当n=k+1时, ,
,
即 ,
,
∴ .
.
由(1)(2)可知对n∈N+,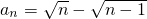 成立.
成立.
分析:(I)由题意可得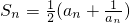 ,令n=1可得a1=1,可求得a2,再由a2的值求 a3的值,并猜想an,
,令n=1可得a1=1,可求得a2,再由a2的值求 a3的值,并猜想an,
(II)猜想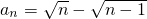 ,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
点评:本题考查数列的递推公式,用数学归纳法证明等式成立.证明当n=k+1时命题也成立,是解题的难点.
 ?
?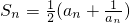
当n=1时,
 ,可得a1=1,
,可得a1=1,当n=2时,
 ,可得
,可得 (an>0),
(an>0),当n=3时,
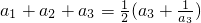 ,可得
,可得 (an>0),
(an>0),猜想:
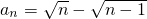 (n∈N+)
(n∈N+)(II)证明:(1)当n=1时,已证.
(2)假设n=k(k≥1)时,
 成立,则当n=k+1时,
成立,则当n=k+1时, ,
,即
 ,
,∴
 .
.由(1)(2)可知对n∈N+,
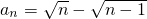 成立.
成立.分析:(I)由题意可得
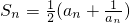 ,令n=1可得a1=1,可求得a2,再由a2的值求 a3的值,并猜想an,
,令n=1可得a1=1,可求得a2,再由a2的值求 a3的值,并猜想an,(II)猜想
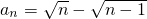 ,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.点评:本题考查数列的递推公式,用数学归纳法证明等式成立.证明当n=k+1时命题也成立,是解题的难点.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目