题目内容
设数列{an}的前n项的和Sn与an的关系是Sn=-an+1-
,n∈N*.
(1)求证:数列{2nan}为等差数列,并求数列{an}的通项;
(2)求数列{Sn}的前n项和Tn.
| 1 |
| 2n |
(1)求证:数列{2nan}为等差数列,并求数列{an}的通项;
(2)求数列{Sn}的前n项和Tn.
(1)当n=1时,s1=-a1+1-
⇒a1=
…(1分),
n≥2时,由Sn-Sn-1=-an+an-1+
,
得2nan-2n-1an-1=
,
∴数列{2nan}为等差数列,…(3分)
∴2nan=2×a1+(n-1)×
,an=
.…(6分)
(2)由(1)得Sn=1-
,
∴Tn=n-(
+
+…+
),①
Tn=
n-(
+
+…+
),②
①-②得
Tn=
n-(
+
+
+…+
-
)
=
n-
-
+
=
n-1+
+
.…(9分)
∴Tn=n-2+
.…(12分)
| 1 |
| 2 |
| 1 |
| 4 |
n≥2时,由Sn-Sn-1=-an+an-1+
| 1 |
| 2n |
得2nan-2n-1an-1=
| 1 |
| 2 |
∴数列{2nan}为等差数列,…(3分)
∴2nan=2×a1+(n-1)×
| 1 |
| 2 |
| n |
| 2n+1 |
(2)由(1)得Sn=1-
| n+2 |
| 2n+1 |
∴Tn=n-(
| 3 |
| 22 |
| 4 |
| 23 |
| n+2 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 23 |
| 4 |
| 24 |
| n+2 |
| 2n+2 |
①-②得
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n+1 |
| n+2 |
| 2n+2 |
=
| 1 |
| 2 |
| 3 |
| 4 |
| ||||
1-
|
| n+2 |
| 2n+2 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 2n+4 |
| 2n+1 |
∴Tn=n-2+
| 2n+5 |
| 2n |

练习册系列答案
相关题目
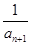 -
-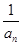 =d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{
=d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{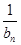 }为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( )
}为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( )