Question

如图，直三棱柱ABC-A₁B₁C₁中，D，E分别是AB，BB₁的中点
（Ⅰ）证明：BC₁∥平面A₁CD
（Ⅱ）AA₁=AC=CB=2，AB=2

2

，求三棱锥C-A₁DE的体积．

Answer 1

分析：（Ⅰ）连接AC₁ 交A₁C于点F，则DF为三角形ABC₁的中位线，故DF∥BC₁．再根据直线和平面平行的判定定理证得
BC₁∥平面A₁CD．
（Ⅱ）由题意可得此直三棱柱的底面ABC为等腰直角三角形，由D为AB的中点可得CD⊥平面ABB₁A₁．求得CD的值，利用
勾股定理求得A₁D、DE和A₁E的值，可得A₁D⊥DE．进而求得S△A1DE的值，再根据三棱锥C-A₁DE的体积
为

1

3

•S△A1DE•CD，运算求得结果．

解答：解：（Ⅰ）证明：连接AC₁ 交A₁C于点F，则F为AC₁的中点．
∵直棱柱ABC-A₁B₁C₁中，D，E分别是AB，BB₁的中点，故DF为三角形ABC₁的中位线，故DF∥BC₁．
由于DF?平面A₁CD，而BC₁不在平面A₁CD中，故有BC₁∥平面A₁CD．

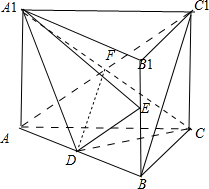
（Ⅱ）∵AA₁=AC=CB=2，AB=2

2

，故此直三棱柱的底面ABC为等腰直角三角形．
由D为AB的中点可得CD⊥平面ABB₁A₁ ，∴CD=

AC•BC

AB

=

2

．
∵A₁D=

A1A2+AD2

=

6

，同理，利用勾股定理求得 DE=

3

，A₁E=3．
再由勾股定理可得A1D2+DE²=A1E2，∴A₁D⊥DE．
∴S△A1DE=

1

2

•A1D•DE=

3 2

2

，
∴VC-A1DE=

1

3

•S△A1DE•CD=1．

点评：本题主要考查直线和平面平行的判定定理的应用，求三棱锥的体积，体现了数形结合的数学思想，属于中档题．