题目内容
如图,A地在B地东偏北45°方向相距2
km处,B地与东西走向的高铁线(近似看成直线)l相距4km.已知曲线形公路PQ上任意一点到B地的距离等于到高铁线l的距离,现要在公路旁建造一个变电房M(变电房与公路之间的距离忽略不计)分别向A地、B地送电.
(Ⅰ)试建立适当的直角坐标系求环形公路PQ所在曲线的轨迹方程;
(Ⅱ)问变电房M应建在相对A地的什么位置(方位和距离),才能使得架设电路所用电线长度最短?并求出最短长度.

| 2 |
(Ⅰ)试建立适当的直角坐标系求环形公路PQ所在曲线的轨迹方程;
(Ⅱ)问变电房M应建在相对A地的什么位置(方位和距离),才能使得架设电路所用电线长度最短?并求出最短长度.

分析:(Ⅰ)取经过点B且垂直l的直线为y轴,垂足为K,并使原点与线段BK的中点重合,建立直角坐标系xoy,由题意可知环形公路PQ所在曲线的轨迹是抛物线,直接利用抛物线的定义得到其标准方程;
(Ⅱ)利用抛物线的定义,把所要求的最小值转化为在抛物线上取一点,使该点到A点的距离和到高铁线l的距离最小.
(Ⅱ)利用抛物线的定义,把所要求的最小值转化为在抛物线上取一点,使该点到A点的距离和到高铁线l的距离最小.
解答:解:(Ⅰ) 如图,

取经过点B且垂直l的直线为y轴,垂足为K,
并使原点与线段BK的中点重合,建立直角坐标系xoy,
则B(0,2),A(2,4),
因为环形公路PQ上任意一点到B地的距离等于到直线l的距离,
所以PQ所在的曲线是以B(0,2)为焦点,l为准线的抛物线.
设抛物线方程为x2=2py(p>0),则p=4.
∴环形公路PQ所在曲线的轨迹方程为x2=8y.
(Ⅱ)要使架设电线长度最短,即|MA|+|MB|最小,
过M作MH⊥l,垂足为H,依题意|MB|=|MH|
∴|MA|+|MB|=|MA|+|MH|,
当A、M、H三点共线时,|MA|+|MH|取得最小值,即|MA|+|MB|取得最小值,
此时M(2,
),位于A地正南方且与A地相距
km,所用电线最短长度为6km.

取经过点B且垂直l的直线为y轴,垂足为K,
并使原点与线段BK的中点重合,建立直角坐标系xoy,
则B(0,2),A(2,4),
因为环形公路PQ上任意一点到B地的距离等于到直线l的距离,
所以PQ所在的曲线是以B(0,2)为焦点,l为准线的抛物线.
设抛物线方程为x2=2py(p>0),则p=4.
∴环形公路PQ所在曲线的轨迹方程为x2=8y.
(Ⅱ)要使架设电线长度最短,即|MA|+|MB|最小,
过M作MH⊥l,垂足为H,依题意|MB|=|MH|
∴|MA|+|MB|=|MA|+|MH|,
当A、M、H三点共线时,|MA|+|MH|取得最小值,即|MA|+|MB|取得最小值,
此时M(2,
| 1 |
| 2 |
| 7 |
| 2 |
点评:本题考查了圆锥曲线的轨迹方程问题,考查了抛物线的定义,体现了数学转化思想方法,解答的关键是正确建立平面直角坐标系,是中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
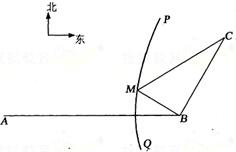 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的没岸PQ(曲线)上任意一点到A的距离比到B的距离远2km.现要在曲线PQ上一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元/km、2a万元/km,那么修建这两条公路的总费用最低是( )
A、(2
| ||
| B、5a万元 | ||
C、(2
| ||
D、(2
|
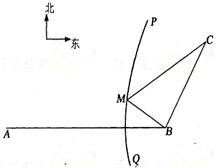 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km..现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.那么这两条公路MB、MC的路程之和最短是
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2km..现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.那么这两条公路MB、MC的路程之和最短是
 km处,B地与东西走向的高铁线(近似看成直线)l相距4km.已知曲线形公路PQ上任意一点到B地的距离等于到高铁线l的距离,现要在公路旁建造一个变电房M(变电房与公路之间的距离忽略不计)分别向A地、B地送电.
km处,B地与东西走向的高铁线(近似看成直线)l相距4km.已知曲线形公路PQ上任意一点到B地的距离等于到高铁线l的距离,现要在公路旁建造一个变电房M(变电房与公路之间的距离忽略不计)分别向A地、B地送电.