题目内容
雾霾大气严重影响人们生活,某科技公司拟投资开发新型节能环保产品,策划部制定投资计划时,不仅要考虑可能获得的盈利,而且还要考虑可能出现的亏损,经过市场调查,公司打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和60%,可能的最大亏损率分别为20%和10%,投资人计划投资金额不超过10万元要求确保可能的资金亏损不超过1.6万元.
(1)若投资人用 万元投资甲项目,
万元投资甲项目, 万元投资乙项目,试写出
万元投资乙项目,试写出 、
、 所满足的条件,并在直角坐标系内做出表示
所满足的条件,并在直角坐标系内做出表示 、
、 范围的图形;
范围的图形;
(2)根据(1)的规划,投资公司对甲、乙两个项目投资多少万元,才能是可能的盈利最大?
(1)如图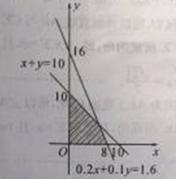 ;
;
(2)用6万元投资甲项目,4万元投资乙项目.
解析试题分析:(1)根据已知条件列出不等式组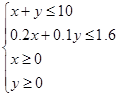 ,再在平面直角坐标系中画出对应的可行域,注意边界上的点也满足条件;(2)主要是利用可行域求解线性目标函数的最大值即得投资公司获得的最大利润,图解法解决含有实际背景的线性规划问题的基本步骤是:①列出约束条件,确定目标函数;②画出不等式(组)表示的平面区域;③作平行直线系使之与可行域有交点,求得最优解;④写出目标函数的最值,并下结论.
,再在平面直角坐标系中画出对应的可行域,注意边界上的点也满足条件;(2)主要是利用可行域求解线性目标函数的最大值即得投资公司获得的最大利润,图解法解决含有实际背景的线性规划问题的基本步骤是:①列出约束条件,确定目标函数;②画出不等式(组)表示的平面区域;③作平行直线系使之与可行域有交点,求得最优解;④写出目标函数的最值,并下结论.
试题解析:(1)由题意,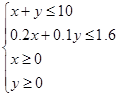 上述不等式组表示的平面区域如图中阴影部分(含边界),
上述不等式组表示的平面区域如图中阴影部分(含边界),
根据(1)的规划和题设条件,可知目标函数为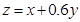 ,作直线
,作直线 ,并作平行于直线
,并作平行于直线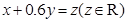 与可行域相交,当平行直线经过直线
与可行域相交,当平行直线经过直线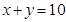 与
与 的交点
的交点 时,其截距最大,解方程组
时,其截距最大,解方程组 ,解得
,解得 ,即
,即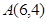 ,
,
此时 (万元),
(万元),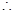 当
当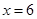 ,
,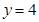 时,
时, 取得最大值.
取得最大值.
即投资人用6万元投资甲项目,4万元投资乙项目,才能确保亏损不超过1.6万元,使可能的利润最大.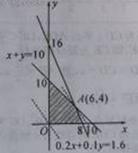
考点:用线性规划解决实际问题,投资利润最大问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案已知不等式 恒成立,则实数m的取值范围是( )
恒成立,则实数m的取值范围是( )
A. | B. |
C. 或 或 | D. 或 或 |
若函数 的最小值3,则实数
的最小值3,则实数 的值为( )
的值为( )
| A.5或8 | B. 或5 或5 | C. 或 或 | D. 或 或 |
已知a,b,c为三角形的三边且S=a2+b2+c2,P=ab+bc+ca,则 ( )
| A.S≥2P | B.P<S<2P |
| C.S>P | D.P≤S<2P |


 不小于6米,则菱形喷水池的两条对角线的长度之和
不小于6米,则菱形喷水池的两条对角线的长度之和 的
的