题目内容
设函数![]() 。
。
(Ⅰ)若在定义域内存在![]() ,而使得不等式
,而使得不等式![]() 能成立,求实数
能成立,求实数![]() 的最小值;
的最小值;
(Ⅱ)若函数![]() 在区间
在区间![]() 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数![]() 的取值范围。
的取值范围。
解:(Ⅰ)要使得不等式![]() 能成立,只需
能成立,只需![]() 。
。
求导得:![]() ,
,
∵函数![]() 得定义域为
得定义域为![]() ,
,
当![]() 时,
时,![]() ,
,
∴函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
当![]() 时,
时,![]() ,
,
∴函数![]() 在区间(0,+∞)上是增函数。
在区间(0,+∞)上是增函数。
∴![]() ,
,
∴![]() 。故实数
。故实数![]() 的最小值为
的最小值为![]() 。
。
(Ⅱ)由![]() 得:
得:
![]()
原题设即方程![]() 在区间
在区间![]() 上恰有两个相异实根。
上恰有两个相异实根。
设![]() 。∵
。∵![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
| - | 0 | + | ||
|
|
| 减函数 |
| 增函数 |
|
∵![]() ,∴
,∴![]() 。
。
从而有![]() ,
,![]()
画出函数![]() 在区间
在区间![]() 上的草图(见下)
上的草图(见下)

易知要使方程![]() 在区间
在区间![]() 上恰有两个相异实根,
上恰有两个相异实根,
只需:![]() ,
,
即:![]() 。
。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
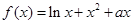 。
。 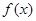 在
在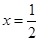 处取得极值,求
处取得极值,求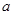 的值;
的值;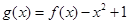 ,当
,当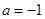 时,
时,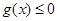 在其定义域内恒成立;
在其定义域内恒成立;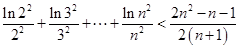 。
。