题目内容
已知函数y=loga(a2x)·
解:由4x-1-5·2x+16≤0得
![]() ·22x-5·2x+16≤0,
·22x-5·2x+16≤0,
∴4≤2x≤16.∴2≤x≤4.
又y=(2+logax)(![]() +
+![]() )
)
=![]() (logax+
(logax+![]() )2-
)2-![]() ,-
,-![]() ≤y≤0,
≤y≤0,
∴-2≤logax≤-1.
(1)当a>1时,a-2≤x≤a-1,由定义域
2≤x≤4,得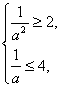
∴![]() ≤a≤
≤a≤![]() ,与a>1矛盾.
,与a>1矛盾.
(2)当0<a<1时,a-1≤x≤a-2,得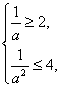
∴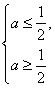 或
或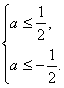
∴a=![]() .
.
综上,得a=![]() .
.

练习册系列答案
相关题目
 7、已知函数y=loga(x+b)的图象如图所示,则a、b的取值范围分别是( )
7、已知函数y=loga(x+b)的图象如图所示,则a、b的取值范围分别是( )