题目内容
已知函数f(x)=x3-ax2+3x+1,
(Ⅰ)设a=2,求f(x)的单调区间;
(Ⅱ)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围.
(Ⅰ)设a=2,求f(x)的单调区间;
(Ⅱ)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围.
解:(Ⅰ)当a=2时,f(x)=x3-6x2+3x+1,
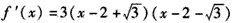 ,
,
当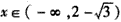 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在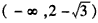 上单调增加;
上单调增加;
当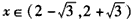 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在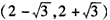 上单调减少;
上单调减少;
当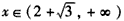 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在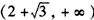 上单调增加;
上单调增加;
综上,f(x)的单调增区间是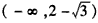 和
和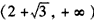 ,f(x)的单调减区间是
,f(x)的单调减区间是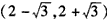 。
。
(Ⅱ)f′(x)=3[(x-a)2+1-a2],
当1-a2≥0时,f′(x)≥0,f(x)为增函数,故f(x)无极值点;
当1-a2<0时,f'′(x)=0有两个根,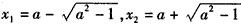 ,
,
由题意,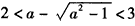 ,①
,①
或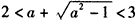 ,②,
,②,
①式无解,②式的解为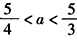 。
。
因此a的取值范围是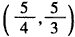 。
。
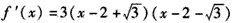 ,
,当
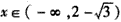 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在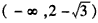 上单调增加;
上单调增加;当
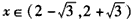 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在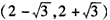 上单调减少;
上单调减少;当
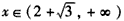 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在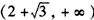 上单调增加;
上单调增加;综上,f(x)的单调增区间是
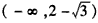 和
和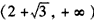 ,f(x)的单调减区间是
,f(x)的单调减区间是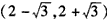 。
。(Ⅱ)f′(x)=3[(x-a)2+1-a2],
当1-a2≥0时,f′(x)≥0,f(x)为增函数,故f(x)无极值点;
当1-a2<0时,f'′(x)=0有两个根,
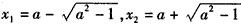 ,
,由题意,
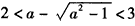 ,①
,①或
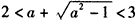 ,②,
,②,①式无解,②式的解为
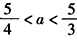 。
。因此a的取值范围是
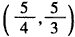 。
。 
练习册系列答案
相关题目