题目内容
设集合A={y|y=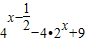
，其中x∈[0，3]}，B={y|y2-（a2+a+1）y+a3+a≥0}，若A∩B=∅，求实数a的取值范围．
【答案】分析：利用二次函数的单调性、指数函数的单调性、一元二次不等式的解法即可得出．
解答：解：y=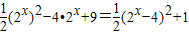
∵x∈[0，3]，∴2x∈[1，8]，
∴A=[1，9]，
y2-（a2+a+1）y+a3+a≥0
∵a2+1＞a
∴B={y|y≤a或y≥a2+1}
∵A∩B=∅
∴a＜1
a2+1＞9
∴a＜-2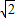
点评：熟练掌握二次函数的单调性、指数函数的单调性、一元二次不等式的解法是解题的关键．
解答：解：y=
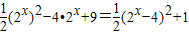
∵x∈[0，3]，∴2x∈[1，8]，
∴A=[1，9]，
y2-（a2+a+1）y+a3+a≥0
∵a2+1＞a
∴B={y|y≤a或y≥a2+1}
∵A∩B=∅
∴a＜1
a2+1＞9
∴a＜-2
点评：熟练掌握二次函数的单调性、指数函数的单调性、一元二次不等式的解法是解题的关键．
练习册系列答案
相关题目
设集合A={y|y=1nx，x≥1}，B={y|y=1-2x，x∈R}则A∩B=（ ）
| A、[0.1） | B、[0，1] | C、（-∞，1] | D、[0，+∞） |