题目内容
已知函数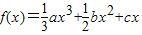 .
.(Ⅰ)若函数f(x)有三个零点x1,x2,x3,且
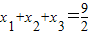 ,x2x3=6,
,x2x3=6,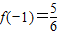 ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;(Ⅱ)若
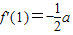 ,3a>2c>2b,求证:导函数f'(x)在区间(0,2)内至少有一个零点;
,3a>2c>2b,求证:导函数f'(x)在区间(0,2)内至少有一个零点;(Ⅲ)在(Ⅱ)的条件下,若导函数f'(x)的两个零点之间的距离不小于
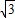 ,求
,求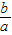 的取值范围.
的取值范围.
【答案】分析:(I)因为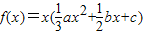 ,因为x2,x3是方程
,因为x2,x3是方程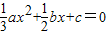 的两根,使用根与系数的关系,再由
的两根,使用根与系数的关系,再由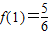 ,求出b、a、c 的值,得到f(x)的 解析式及f'(x)的解析式,由f'(x)<0求出减区间.
,求出b、a、c 的值,得到f(x)的 解析式及f'(x)的解析式,由f'(x)<0求出减区间.
(Ⅱ) 求出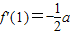 ,f'(0)=c,f'(2)=a-c,当c>0时 f'(x)在区间(0,1)内至少有一个零点,当c≤0时,f'(x)在区间(1,2)内至少有一零点.
,f'(0)=c,f'(2)=a-c,当c>0时 f'(x)在区间(0,1)内至少有一个零点,当c≤0时,f'(x)在区间(1,2)内至少有一零点.
(Ⅲ)设m,n是导函数f'(x)=ax2+bx+c的两个零点,由|m-n|≥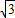 ,及 3a>2c>2b,a>0 求出
,及 3a>2c>2b,a>0 求出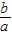 的取值范围.
的取值范围.
解答:解:(I)因为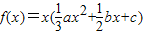 ,又
,又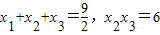 ,则
,则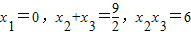 .
.
因为x2,x3是方程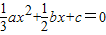 的两根,则
的两根,则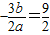 ,
,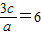 .即b=-3a,c=2a.
.即b=-3a,c=2a.
又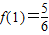 ,即
,即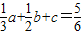 ,所以,
,所以,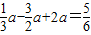 ,即a=1,从而b=-3,c=2.
,即a=1,从而b=-3,c=2.
所以,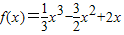 . 因为f'(x)=x2-3x+2,由x2-3x+2<0,得1<x<2.
. 因为f'(x)=x2-3x+2,由x2-3x+2<0,得1<x<2.
故f(x)的单调递减区间是(1,2),单调递增区间是(-∞,1),(2+∞).
(Ⅱ)因为f'(x)=ax2+bx+c,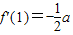 ,所以
,所以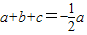 ,即3a+2b+2c=0.
,即3a+2b+2c=0.
因为3a>2c>2b,所以3a>0,2b<0,即a>0,b<0.
于是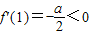 ,f'(0)=c,f'(2)=4a+2b+c=4a-(3a+2c)+c=a-c.
,f'(0)=c,f'(2)=4a+2b+c=4a-(3a+2c)+c=a-c.
(1)当c>0时,因为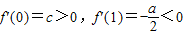 ,则f'(x)在区间(0,1)内至少有一个零点.
,则f'(x)在区间(0,1)内至少有一个零点.
(2)当c≤0时,因为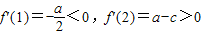 ,则f'(x)在区间(1,2)内至少有一零点.
,则f'(x)在区间(1,2)内至少有一零点.
故导函数f'(x)在区间(0,2)内至少有一个零点.
(Ⅲ)设m,n是导函数f'(x)=ax2+bx+c的两个零点,则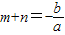 ,
,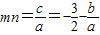 .
.
所以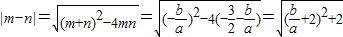 .
.
由已知,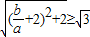 ,则
,则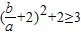 ,即
,即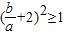 .
.
所以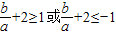 ,即
,即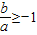 或
或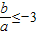 .
.
又2c=-3a-2b,3a>2c>2b,所以,3a>-3a-2b>2b,即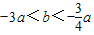 .
.
因为a>0,所以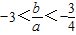 .
.
综上分析,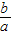 的取值范围是
的取值范围是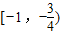 .
.
点评:本题考查利用导数判断函数的单调性,函数的零点的判断,二次函数的性质与不等式性质的应用.
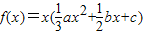 ,因为x2,x3是方程
,因为x2,x3是方程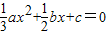 的两根,使用根与系数的关系,再由
的两根,使用根与系数的关系,再由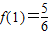 ,求出b、a、c 的值,得到f(x)的 解析式及f'(x)的解析式,由f'(x)<0求出减区间.
,求出b、a、c 的值,得到f(x)的 解析式及f'(x)的解析式,由f'(x)<0求出减区间.(Ⅱ) 求出
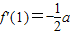 ,f'(0)=c,f'(2)=a-c,当c>0时 f'(x)在区间(0,1)内至少有一个零点,当c≤0时,f'(x)在区间(1,2)内至少有一零点.
,f'(0)=c,f'(2)=a-c,当c>0时 f'(x)在区间(0,1)内至少有一个零点,当c≤0时,f'(x)在区间(1,2)内至少有一零点.(Ⅲ)设m,n是导函数f'(x)=ax2+bx+c的两个零点,由|m-n|≥
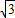 ,及 3a>2c>2b,a>0 求出
,及 3a>2c>2b,a>0 求出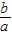 的取值范围.
的取值范围.解答:解:(I)因为
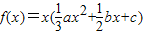 ,又
,又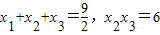 ,则
,则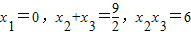 .
.因为x2,x3是方程
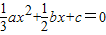 的两根,则
的两根,则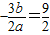 ,
,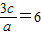 .即b=-3a,c=2a.
.即b=-3a,c=2a.又
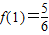 ,即
,即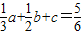 ,所以,
,所以,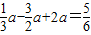 ,即a=1,从而b=-3,c=2.
,即a=1,从而b=-3,c=2.所以,
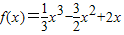 . 因为f'(x)=x2-3x+2,由x2-3x+2<0,得1<x<2.
. 因为f'(x)=x2-3x+2,由x2-3x+2<0,得1<x<2.故f(x)的单调递减区间是(1,2),单调递增区间是(-∞,1),(2+∞).
(Ⅱ)因为f'(x)=ax2+bx+c,
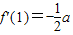 ,所以
,所以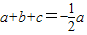 ,即3a+2b+2c=0.
,即3a+2b+2c=0.因为3a>2c>2b,所以3a>0,2b<0,即a>0,b<0.
于是
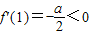 ,f'(0)=c,f'(2)=4a+2b+c=4a-(3a+2c)+c=a-c.
,f'(0)=c,f'(2)=4a+2b+c=4a-(3a+2c)+c=a-c.(1)当c>0时,因为
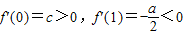 ,则f'(x)在区间(0,1)内至少有一个零点.
,则f'(x)在区间(0,1)内至少有一个零点.(2)当c≤0时,因为
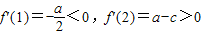 ,则f'(x)在区间(1,2)内至少有一零点.
,则f'(x)在区间(1,2)内至少有一零点.故导函数f'(x)在区间(0,2)内至少有一个零点.
(Ⅲ)设m,n是导函数f'(x)=ax2+bx+c的两个零点,则
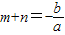 ,
,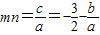 .
.所以
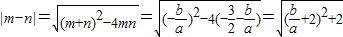 .
.由已知,
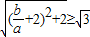 ,则
,则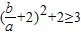 ,即
,即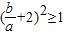 .
.所以
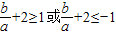 ,即
,即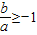 或
或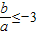 .
.又2c=-3a-2b,3a>2c>2b,所以,3a>-3a-2b>2b,即
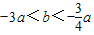 .
.因为a>0,所以
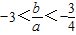 .
.综上分析,
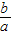 的取值范围是
的取值范围是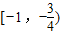 .
.点评:本题考查利用导数判断函数的单调性,函数的零点的判断,二次函数的性质与不等式性质的应用.

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数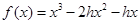 ,若
,若 且
且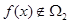 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得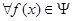 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“二阶比增函数”.
为“二阶比增函数”.
我们把所有“一阶比增函数”组成的集合记为![]() ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为![]() .
.
(Ⅰ)已知函数![]() ,若
,若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)已知![]() ,
,![]() 且
且![]() 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证:![]() ;
;
(Ⅲ)定义集合![]()
请问:是否存在常数![]() ,使得
,使得![]() ,
,![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“二阶比增函数”.
为“二阶比增函数”.
我们把所有“一阶比增函数”组成的集合记为![]() ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为![]() .
.
(Ⅰ)已知函数![]() ,若
,若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)已知![]() ,
,![]() 且
且![]() 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
求证:![]() ;
;
(Ⅲ)定义集合![]()
请问:是否存在常数![]() ,使得
,使得![]() ,
,![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


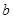
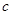




 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.