Question

【题目】设函数f（x）=x2﹣ax（a＞0，且a≠1），g（x）=f′（x）（其中f′（x）为f（x）的导函数）．
（1）当a=e时，求g（x）的极大值点；
（2）讨论f（x）的零点个数．

Answer 1

【答案】
（1）解：a=e时，g（x）=2x﹣ex，g′（x）=2﹣ex，

令g′（x）=0得：2﹣ex=0，解得x=ln2，

∴当x＜ln2时，g′（x）＞0；当x＞ln2时，g′（x）＜0，

∴g（x）的极大值点为ln2．

（2）解：（Ⅰ）当a＞1时，f′（x）=2x﹣lnaax，

∴当x≤0时，f′（x）＜0，∴f（x）在（﹣∞，0）上为减函数，

∵f（﹣1）=1﹣ ＞0，f（0）=﹣1＜0，

∴f（x）在（0，+∞）有一个零点；

当x＞0时，令f（x）=0得x2=ax，即lna= ，

令h（x）= ，则h′（x）= ．

∴当0＜x＜e时，h′（x）＞0；当x＞e时，h′（x）＜0，

∴h（x）在（0，e）上单调递增，在（e，+∞）上单调递减，

做出y=h（x）的图象如下图，

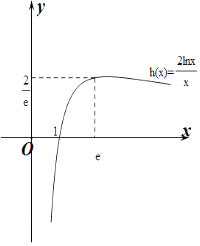
由图象可知：

①当lna＞ 即a＞e 时，f（x）在（0，+∞）上无零点；

②当lna= 即a=e 时，f（x）在（0，+∞）上有1个零点；

③当0＜lna＜ 即1＜a＜e 时，f（x）在（0，+∞）上有2个零点；

（Ⅱ）当0＜a＜1时，f′（x）=2x﹣lnaax，

∴当 x＞0时，f′（x）＞0，∴f（x）在（0，+∞）上是增函数，

∵f（0）=﹣l＜0，f（1）=1﹣a＞0，

∴f（x）在（0，+∞）上有1个零点；

当x＜0时，令f（x）=0得lna= ，

令H（x）= ，则H′（x）= ，

∴当﹣e＜x＜0时，H′（x）＞0，当x＜﹣e时，H′（x）＜0，

∴H（x）在（﹣∞，﹣e）上单调递减，在（﹣e，0）上单调递增，

作出y=H（x）的函数图象如图：

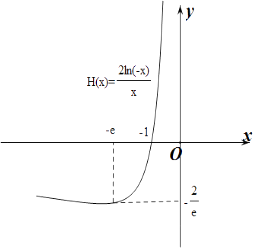
由图象可知：

当lna＜﹣ 即0 时，f（x）在（﹣∞，0）上无零点；

当lna=﹣ 即a=e 时，f（x）在（﹣∞，0）上有1个零点；

当﹣ ＜lna＜0即e ＜a＜1时，f（x）在（﹣∞，0）上有2个零点；

综上：

①当0＜a＜e 或a＞e 时，f（x）有1个零点；

②当a=e 或a=e 时，f（x）有2个零点；

③当e ＜a＜1或1＜a＜e 时，f（x）有3个零点．

【解析】（1）令g′（x）=0求出g（x）的极值点，判断g′（x）的符号变化即可得出答案；（2）f′（x）=2x﹣lnaax ， 对a和x进行讨论，利用零点的存在性定理，结合函数的图象判断零点的个数．
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值才能正确解答此题．