题目内容
已知函数f(x)=3x2-2x+1,g(x)=ax2,对任意的正实数x,f(x)≥g(x)恒成立,则实数a的取值范围是________.
a≤2
分析:由已知,不等式x2-2ax+1≥0恒成立,即不等式a≤ 对任意的正实数x恒成立.设a(x)=
对任意的正实数x恒成立.设a(x)= ,即a(x)=3-
,即a(x)=3- +
+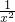 ,将
,将 看成整体,利用二次函数的性质求出它的最小值为2,从而得出实数a的取值范围.
看成整体,利用二次函数的性质求出它的最小值为2,从而得出实数a的取值范围.
解答:不等式f(x)≥g(x)
即3x2-2x+1≥ax2对任意的正实数x恒成立,
即不等式a≤ 对任意的正实数x恒成立.
对任意的正实数x恒成立.
设a(x)= ,即a(x)=3-
,即a(x)=3- +
+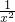 ,当x>0时,它的最小值为2,
,当x>0时,它的最小值为2,
∴a≤2
故答案为a≤2.
点评:本题考查不等式(函数)恒成立问题.由于本题是二次不等式,故采用数形结合的思想,利用根据二次函数图象与二次不等式解的关系来解决.要掌握好“三个二次”的关系,以及其中蕴含的数形结合、转化的思想方法.
分析:由已知,不等式x2-2ax+1≥0恒成立,即不等式a≤
 对任意的正实数x恒成立.设a(x)=
对任意的正实数x恒成立.设a(x)= ,即a(x)=3-
,即a(x)=3- +
+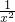 ,将
,将 看成整体,利用二次函数的性质求出它的最小值为2,从而得出实数a的取值范围.
看成整体,利用二次函数的性质求出它的最小值为2,从而得出实数a的取值范围.解答:不等式f(x)≥g(x)
即3x2-2x+1≥ax2对任意的正实数x恒成立,
即不等式a≤
 对任意的正实数x恒成立.
对任意的正实数x恒成立.设a(x)=
 ,即a(x)=3-
,即a(x)=3- +
+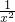 ,当x>0时,它的最小值为2,
,当x>0时,它的最小值为2,∴a≤2
故答案为a≤2.
点评:本题考查不等式(函数)恒成立问题.由于本题是二次不等式,故采用数形结合的思想,利用根据二次函数图象与二次不等式解的关系来解决.要掌握好“三个二次”的关系,以及其中蕴含的数形结合、转化的思想方法.

练习册系列答案
相关题目
已知函数f(x)=3•2x-1,则当x∈N时,数列{f(n+1)-f(n)}( )
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |