Question

【题目】

已知数列和满足：,，，其中为实数，为正整数.

（Ⅰ）对任意实数，证明:数列不是等比数列；

（Ⅱ）证明：当时，数列是等比数列；

（Ⅲ）设（为实常数）,为数列的前项和.是否存在实数，使得对任意正整数，都有?若存在，求的取值范围；若不存在，说明理由.

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ）证明见解析；（Ⅲ）存在，

【解析】

解： （Ⅰ）证明：假设存在一个实数，使｛an｝是等比数列，则有

即（）2=2矛盾.

所以｛an｝不是等比数列.

(Ⅱ)解：因为bn+1=(-1)n+1［an+1-3(n-1)+21］=(-1)n+1(an-2n+14)

=-(-1)n·（an-3n+21）=-bn

当λ≠－18时，b1="-(λ+18)" ≠0,由上可知bn≠0，∴(n∈N+).

故当λ≠-18时，数列｛bn｝是以－（λ＋18）为首项，－为公比的等比数列；

（Ⅲ)由（2）知，当λ=-18,bn=0,Sn=0,不满足题目要求.

∴λ≠-18，故知bn= -（λ+18）·（－）n-1，于是可得

Sn=-

要使a<Sn<b对任意正整数n成立，

即a<-(λ+18)·［1－（－）n］<b(n∈N+) ,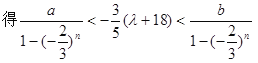

当n为正奇数时，1<f(n)

∴f(n)的最大值为f(1)=, f(n)的最小值为f(2)=,

于是，由①式得

当a<b3a时，由，不存在实数满足要求

当b>3a存在λ，使得对任意正整数n,都有a<Sn<b,且λ的取值范围是）