题目内容
（2012•广东模拟）已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=
，三内角A，B，C成等差数列，则sinA=
．
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
分析：由三角形的三个内角成等差数列，利用等差数列的性质及三角形的内角和定理求出B的度数，进而得出sinB的值，再由a与b的值，利用正弦定理即可求出sinA的值．
解答：解：∵三角形内角A，B，C成等差数列，
∴A+C=2B，又A+B+C=π，
∴B=
，又a=1，b=
，
则根据正弦定理
=
得：sinA=
=
．
故答案为：
∴A+C=2B，又A+B+C=π，
∴B=
| π |
| 3 |
| 3 |
则根据正弦定理
| a |
| sinA |
| b |
| sinB |
| asinB |
| b |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：此题考查了等差数列的性质，正弦定理，以及特殊角的三角函数值，熟练掌握定理及性质是解本题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
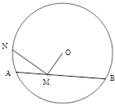（2012•广东模拟）（几何证明选讲选做题）如图，点M为⊙O的弦AB上的一点，连接MO．MN⊥OM，MN交圆于N，若MA=2，MB=4，则MN=