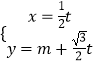[题目]数列{an}的各项均为正数.其前n项和为Sn . 已知 =1.且a1= .则tanSn的取值集合是( )A.{0. }B.{0. . }C.{0. .﹣ }D.{0. .﹣ } 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】数列{an}的各项均为正数，其前n项和为Sn ，已知 =1，且a1= ，则tanSn的取值集合是（）
A.{0， }
B.{0，， }
C.{0，，﹣ }
D.{0，，﹣ }

【答案】A
【解析】解：∵ =1，∴na =（n+1）a +anan+1 ， ∴[nan+1﹣（n+1）an]（an+1+an）=0，an ， an+1＞0． ∴nan+1﹣（n+1）an=0，即．
∴ =…= = ．
∴an= ×n．
∴Sn= ．
∴tanSn=tan[ ]，
n=3k∈N*时，tanSn= =0；
n=3k﹣1∈N*时，tanSn=tan =0；
n=3k﹣2∈N*时，tanSn=tan π= ．
综上可得：tanSn的取值集合是{0， }．
故选：A．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系)．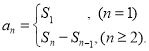

练习册系列答案

相关题目

【题目】设函数f（x）=2x﹣a，g（x）=x+2．
（1）当a=1时，求不等式f（x）+f（﹣x）≤g（x）的解集；
（2）求证：中至少有一个不小于．

【题目】（14分）已知a，b为常数，且a≠0，函数f（x）=﹣ax+b+axlnx，f（e）=2（e=2.71828…是自然对数的底数）．

（I）求实数b的值；

（II）求函数f（x）的单调区间；

（III）当a=1时，是否同时存在实数m和M（m＜M），使得对每一个t∈[m，M]，直线y=t与曲线y=f（x）（x∈[，e]）都有公共点？若存在，求出最小的实数m和最大的实数M；若不存在，说明理由．

【题目】在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
（1）若直线l与曲线C没有公共点，求m的取值范围；
（2）若m=0，求直线l被曲线C截得的弦长．

【题目】据统计，某地区植被覆盖面积公顷与当地气温下降的度数之间呈线性相关关系，对应数据如下：

公顷	20	40	60	80
	3	4	4	5

请用最小二乘法求出y关于x的线性回归方程；

根据中所求线性回归方程，如果植被覆盖面积为300公顷，那么下降的气温大约是多少？

参考公式：线性回归方程；其中，．

【题目】已知F1 ， F2是双曲线C1： ﹣ =1（a＞0，b＞0）的左、右焦点，且F2是抛物线C2：y2=2px（p＞0）的焦点，P是双曲线C1与抛物线C2在第一象限内的交点，线段PF2的中点为M，且|OM|= |F1F2|，其中O为坐标原点，则双曲线C1的离心率是（）
A.2+
B.1+
C.2+
D.1+

【题目】为了更好地了解鲸的生活习性，某动物保护组织在受伤的鲸身上安装了电子监测设备，从海岸线放归点处把它放归大海，并沿海岸线由西到东不停地对其进行跟踪观测。在放归点的正东方向有一观测站，可以对鲸进行生活习性的详细观测。已知，观测站的观测半径为.现以点为坐标原点、以由西向东的海岸线所在直线为轴建立平面直角坐标系，则可以测得鲸的行进路线近似的满足.