题目内容
点M(x,y)与定点(3,0)的距离和它到定直线l:x=
思路分析:利用已知曲线求方程的一般方法,先求出方程,再根据方程指出曲线的形状.
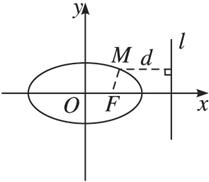
解:如图,设d是点M到直线l:x=![]() 的距离,根据题意,点M的轨迹就是集合P={M|
的距离,根据题意,点M的轨迹就是集合P={M|![]() }.
}.
由此得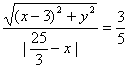 .
.
将上式两边平方并化简,得16x2+25y2=400,
即![]() =1.
=1.
所以点M的轨迹是长轴长、短轴长分别为10、8的椭圆.
温馨提示
椭圆![]() =1的离心率为e=
=1的离心率为e=![]() .通过此例可以看出椭圆
.通过此例可以看出椭圆![]() =1上任意一点M到焦点F(3,0)的距离与M到直线l:x=
=1上任意一点M到焦点F(3,0)的距离与M到直线l:x=![]() 的距离的比值为离心率e.一般地,点M(x,y)与定点F(c,0)的距离和它到定直线l:x=
的距离的比值为离心率e.一般地,点M(x,y)与定点F(c,0)的距离和它到定直线l:x=![]() 的距离的比是常数
的距离的比是常数![]() (a>c>0),则点M的轨迹是椭圆,方程为
(a>c>0),则点M的轨迹是椭圆,方程为![]() =1(b2=a2-c2).因此,椭圆可以看作动点M到定点F的距离与它到定直线的距离的比为常数e(0<e<1)的M的轨迹,这就是椭圆的第二定义.
=1(b2=a2-c2).因此,椭圆可以看作动点M到定点F的距离与它到定直线的距离的比为常数e(0<e<1)的M的轨迹,这就是椭圆的第二定义.

练习册系列答案
相关题目