题目内容
已知等差数列{an}的公差为2,其前n项和Sn=pn2+2n(n∈N*).
(Ⅰ)求p的值及an;
(Ⅱ)若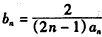 ,记数列{bn}的前n项和为Tn,求使Tn>
,记数列{bn}的前n项和为Tn,求使Tn>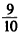 成立的最小正整数n的值。
成立的最小正整数n的值。
(Ⅰ)求p的值及an;
(Ⅱ)若
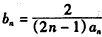 ,记数列{bn}的前n项和为Tn,求使Tn>
,记数列{bn}的前n项和为Tn,求使Tn>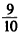 成立的最小正整数n的值。
成立的最小正整数n的值。 解:(Ⅰ)∵{an}是等差数列,
∴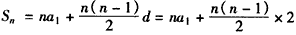
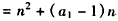 ,
,
又由已知Sn=pn2+2n,
∴p=1,a1-1=2,
∴a1=3,
∴an=a1+(n-1)d=2n+1,
∴p=1,an=2n+1。
(Ⅱ)由(Ⅰ)知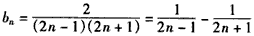 ,
,
∴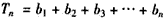
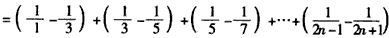
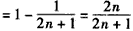 ,
,
又∵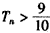 ,
,
∴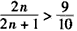 ,∴20n>18n+9,即
,∴20n>18n+9,即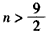 ,
,
又n∈N*,
∴使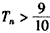 成立的最小正整数的n值为5。
成立的最小正整数的n值为5。
∴
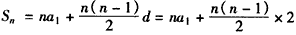
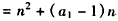 ,
,又由已知Sn=pn2+2n,
∴p=1,a1-1=2,
∴a1=3,
∴an=a1+(n-1)d=2n+1,
∴p=1,an=2n+1。
(Ⅱ)由(Ⅰ)知
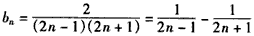 ,
,∴
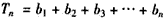
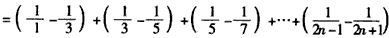
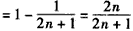 ,
,又∵
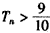 ,
,∴
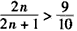 ,∴20n>18n+9,即
,∴20n>18n+9,即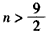 ,
,又n∈N*,
∴使
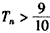 成立的最小正整数的n值为5。
成立的最小正整数的n值为5。 
练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.