题目内容
某公园有甲、乙两个相邻景点,原拟定甲景点内有2个A班的同学和2个B班的同学;乙景点内有2个A班同学和3个B班同学,后由于某种原因甲、乙两景点各有一个同学交换景点观光.(1)求甲景点恰有2个A班同学的概率;
(2)求甲景点A班同学数X的分布列及期望.
解:(1)甲、乙两景点各有一个同学交换后,甲景点恰有2个A班同学有下面几种情况:
①互换的A班同学,则此时甲景点恰好有2个A班同学的事件记为A1,则P(A1)=![]() .
.
②互换的是B班同学,则此时甲景点恰有2个A班同学的事件记为A2,则P(A2)=![]() .
.
故P=P(A1)+P(A2)= ![]() +
+![]() =
=![]() .
.
(2)设甲景点内A班同学数为X,则X的分布列为:
X | 1 | 2 | 3 |
P |
|
|
|
EX=![]() ×1+
×1+![]() ×2+
×2+![]() ×3=
×3=![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
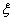 的分布列及数学期望。
的分布列及数学期望。