题目内容
已知函数f(x)=4x3+3tx2-6t2x+t-1,x∈R,其中t∈R.
(1)当t=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)当t≠0时,求f(x)的单调区间.
解:(1))当t=1时,f(x)=4x3+3x2-6x,f(0)=0,f'(x)=12x2+6x-6(2分)f'(0)=-6.所以曲线y=f(x)在点(0,f(0))处的切线方程为y=-6x.(4分)
(2)解:f'(x)=12x2+6tx-6t2,令f'(x)=0,解得x=-t或 .(5分)
.(5分)
因为t≠0,以下分两种情况讨论:
(i)若t<0,则t<0,则 ,当x变化时,f'(x),f(x)的变化情况如下表:
,当x变化时,f'(x),f(x)的变化情况如下表:
所以,f(x)的单调递增区间是 的单调递减区间是
的单调递减区间是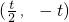 . (8分)
. (8分)
(ii)若 ,当x变化时,f'(x),f(x)的变化情况如下表:
,当x变化时,f'(x),f(x)的变化情况如下表:
所以,f(x)的单调递增区间是 的单调递减区间是
的单调递减区间是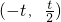 .(12分)
.(12分)
分析:(1)当t=1时,求出函数f(x),利用导数的几何意义求出x=0处的切线的斜率,利用点斜式求出切线方程;
(2)根据f'(0)=0,解得x=-t或x= ,讨论t的正负,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0求出单调区间即可.
,讨论t的正负,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0求出单调区间即可.
点评:本题主要考查了导数的几何意义,利用导数研究函数的单调性、曲线的切线方程、函数零点、解不等式等基础知识,考查了计算能力和分类讨论的思想.
(2)解:f'(x)=12x2+6tx-6t2,令f'(x)=0,解得x=-t或
 .(5分)
.(5分)因为t≠0,以下分两种情况讨论:
(i)若t<0,则t<0,则
 ,当x变化时,f'(x),f(x)的变化情况如下表:
,当x变化时,f'(x),f(x)的变化情况如下表:| x |  | 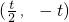 | (-t,+∞) |
| f'(x) | + | - | + |
| f(x) | ↑ | ↓ | ↑ |
 的单调递减区间是
的单调递减区间是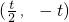 . (8分)
. (8分)(ii)若
 ,当x变化时,f'(x),f(x)的变化情况如下表:
,当x变化时,f'(x),f(x)的变化情况如下表:| x | (-∞,t) | 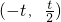 | 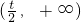 |
| f'(x) | + | - | + |
| f(x) | ↑ | ↓ | ↑ |
 的单调递减区间是
的单调递减区间是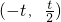 .(12分)
.(12分)分析:(1)当t=1时,求出函数f(x),利用导数的几何意义求出x=0处的切线的斜率,利用点斜式求出切线方程;
(2)根据f'(0)=0,解得x=-t或x=
 ,讨论t的正负,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0求出单调区间即可.
,讨论t的正负,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0求出单调区间即可.点评:本题主要考查了导数的几何意义,利用导数研究函数的单调性、曲线的切线方程、函数零点、解不等式等基础知识,考查了计算能力和分类讨论的思想.

练习册系列答案
相关题目