题目内容
已知函数f(x)=logmx(mm为常数,0<m<1),且数列{f(an)}是首项为2,公差为2的等差数列.
(1)若bn=an•f(an),当m= 时,求数列{bn}的前n项和Sn;
时,求数列{bn}的前n项和Sn;
(2)设cn=an•lgan,如果{cn}中的每一项恒小于它后面的项,求m的取值范围.
解:(1)由题意得f(an)=2+2(n-1)=logman,可得2n=logman,…(1分)
∴an=m2n.…(2分)
bn=an•f(an)=2n•m2n.
∵m= ,∴bn=an•f(an)=2n•(
,∴bn=an•f(an)=2n•( )2n=n•(
)2n=n•( )n-1,…(3分)
)n-1,…(3分)
∴Sn=1•( )0+2•(
)0+2•( )1+3•(
)1+3•( )2+…+n•(
)2+…+n•( )n-1,①
)n-1,①
 Sn=1•(
Sn=1•( )1+2•(
)1+2•( )2+3•(
)2+3•( )3+…+n•(
)3+…+n•( )n,②…(4分)
)n,②…(4分)
①-②,得 Sn=(
Sn=( )0+(
)0+( )1+(
)1+( )2+…+(
)2+…+( )n-1-n•(
)n-1-n•( )n=
)n=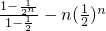 …(6分)
…(6分)
∴化简得:Sn=-(n+2)( )n-1+4 …(7分)
)n-1+4 …(7分)
(2)解:由(Ⅰ)知,cn=an•lgan=2n•m2nlgm,要使cn<cn+1对一切n∈N*成立,
即nlgm<(n+1)m2lgm对一切n∈N*成立.…(8分)
∵0<m<1,可得lgm<0
∴原不等式转化为n>(n+1)m2,对一切n∈N*成立,
只需m2<( )min即可,…(10分)
)min即可,…(10分)
∵h(n)= 在正整数范围内是增函数,∴当n=1时,(
在正整数范围内是增函数,∴当n=1时,( )min=
)min= .…(12分)
.…(12分)
∴m2< ,且0<m<1,,∴0<m<
,且0<m<1,,∴0<m< .…(13分)
.…(13分)
综上所述,存在实数m∈(0, )满足条件.…(14分)
)满足条件.…(14分)
分析:(1)用等差数列求和公式,结合对数的运算性质可得:an=m2n,从而有bn=n•( )n-1,最后用错位相减法结合等比数列的求和公式,得到数列{bn}的前n项和Sn;
)n-1,最后用错位相减法结合等比数列的求和公式,得到数列{bn}的前n项和Sn;
(2)由题意,不等式cn<cn+1对一切n∈N*成立,代入an的表达式并化简可得m2<( )min.通过讨论单调性可得当n=1时,
)min.通过讨论单调性可得当n=1时, 的最小值是
的最小值是 ,从而得到m2<
,从而得到m2< ,结合0<m<1,得到实数m的取值范围是(0,
,结合0<m<1,得到实数m的取值范围是(0, ).
).
点评:本题以对数运算和数列通项与求和运算为载体,求数列的前n项和并求数列单调递增时参数的取值范围,着重考查了等差、等比数列的通项公式与求和公式,以及不等式恒成立问题的讨论等知识,属于中档题.
∴an=m2n.…(2分)
bn=an•f(an)=2n•m2n.
∵m=
 ,∴bn=an•f(an)=2n•(
,∴bn=an•f(an)=2n•( )2n=n•(
)2n=n•( )n-1,…(3分)
)n-1,…(3分)∴Sn=1•(
 )0+2•(
)0+2•( )1+3•(
)1+3•( )2+…+n•(
)2+…+n•( )n-1,①
)n-1,① Sn=1•(
Sn=1•( )1+2•(
)1+2•( )2+3•(
)2+3•( )3+…+n•(
)3+…+n•( )n,②…(4分)
)n,②…(4分)①-②,得
 Sn=(
Sn=( )0+(
)0+( )1+(
)1+( )2+…+(
)2+…+( )n-1-n•(
)n-1-n•( )n=
)n=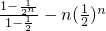 …(6分)
…(6分)∴化简得:Sn=-(n+2)(
 )n-1+4 …(7分)
)n-1+4 …(7分)(2)解:由(Ⅰ)知,cn=an•lgan=2n•m2nlgm,要使cn<cn+1对一切n∈N*成立,
即nlgm<(n+1)m2lgm对一切n∈N*成立.…(8分)
∵0<m<1,可得lgm<0
∴原不等式转化为n>(n+1)m2,对一切n∈N*成立,
只需m2<(
 )min即可,…(10分)
)min即可,…(10分)∵h(n)=
 在正整数范围内是增函数,∴当n=1时,(
在正整数范围内是增函数,∴当n=1时,( )min=
)min= .…(12分)
.…(12分)∴m2<
 ,且0<m<1,,∴0<m<
,且0<m<1,,∴0<m< .…(13分)
.…(13分)综上所述,存在实数m∈(0,
 )满足条件.…(14分)
)满足条件.…(14分)分析:(1)用等差数列求和公式,结合对数的运算性质可得:an=m2n,从而有bn=n•(
 )n-1,最后用错位相减法结合等比数列的求和公式,得到数列{bn}的前n项和Sn;
)n-1,最后用错位相减法结合等比数列的求和公式,得到数列{bn}的前n项和Sn;(2)由题意,不等式cn<cn+1对一切n∈N*成立,代入an的表达式并化简可得m2<(
 )min.通过讨论单调性可得当n=1时,
)min.通过讨论单调性可得当n=1时, 的最小值是
的最小值是 ,从而得到m2<
,从而得到m2< ,结合0<m<1,得到实数m的取值范围是(0,
,结合0<m<1,得到实数m的取值范围是(0, ).
).点评:本题以对数运算和数列通项与求和运算为载体,求数列的前n项和并求数列单调递增时参数的取值范围,着重考查了等差、等比数列的通项公式与求和公式,以及不等式恒成立问题的讨论等知识,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目