题目内容
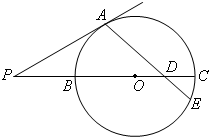
如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B,C两点,D是OC的中点,连接AD并延长交⊙O于点E,若PA=2
| 3 |
分析:连接OA,由AP为圆的切线,得到∠PAO=90°,过A作AM垂直于AC,过O作OF垂直于AE,根据垂径定理得到F为AE的中点,在直角三角形APO中,由AP的长及∠APO的度数,利用正切函数定义及特殊角的三角函数值求出半径OA的长,由D为OC的中点,可求出OD的长,同时得到∠AOD的度数,在三角形AOD中,根据余弦定理求出AD的长,再由OD及边上的高AM求出三角形AOD的面积,此三角形的面积还可以用AD及边上的高OF表示,进而求出OF的长,在直角三角形AOF中,由OA和OF的长,利用勾股定理求出AF的长,进而求出AE的长.
解答: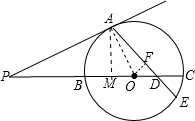 解:连接OA,过O作OF⊥AE,过A作AM⊥PC,如图所示,
解:连接OA,过O作OF⊥AE,过A作AM⊥PC,如图所示,
∵PA为圆O的切线,
∴∠PAO=90°,又PA=2
,∠APB=30°,∴∠AOD=120°,
∴OA=PAtan30°=2
×
=2,又D为OC中点,故OD=1,
根据余弦定理得:AD2=OA2+OD2-2OA•ODcos∠AOD=4+1+2=7,解得:AD=
,
∵在Rt△APM中,∠APM=30°,且AP=2
,
∴AM=
AP=
,
故三角形AOD的面积S=
OD•AM=
,则S=
AD•OF=
OF=
,
∴OF=
,
在Rt△AOF中,根据勾股定理得:AF=
=
,
则AE=2AF=
.
故答案为:
 解:连接OA,过O作OF⊥AE,过A作AM⊥PC,如图所示,
解:连接OA,过O作OF⊥AE,过A作AM⊥PC,如图所示,∵PA为圆O的切线,
∴∠PAO=90°,又PA=2
| 3 |
∴OA=PAtan30°=2
| 3 |
| ||
| 3 |
根据余弦定理得:AD2=OA2+OD2-2OA•ODcos∠AOD=4+1+2=7,解得:AD=
| 7 |
∵在Rt△APM中,∠APM=30°,且AP=2
| 3 |
∴AM=
| 1 |
| 2 |
| 3 |
故三角形AOD的面积S=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴OF=
| ||
| 7 |
在Rt△AOF中,根据勾股定理得:AF=
| OA2-OF2 |
5
| ||
| 7 |
则AE=2AF=
10
| ||
| 7 |
故答案为:
10
| ||
| 7 |
点评:此题考查了直线与圆的位置关系,涉及的知识有锐角三角函数,勾股定理,直角三角形的性质,以及垂径定理,利用了数形结合的思想,直线与圆相切时,常常连接圆心与切点,构造直角三角形解决问题,直线与圆相交时,常常由弦心距,弦的一半及圆的半径构造直角三角形解决问题,学生做此类题应注意辅助线的作法.

练习册系列答案
相关题目
 如图,已知PA是⊙O的切线,切点为A,PC交⊙O于B、C两点,PB=2,BC=6,
如图,已知PA是⊙O的切线,切点为A,PC交⊙O于B、C两点,PB=2,BC=6,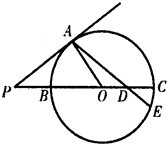 选修4-1:几何证明选讲
选修4-1:几何证明选讲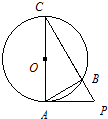
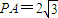 ,∠APB=30°,则AE= .
,∠APB=30°,则AE= .