题目内容
下列命题是真命题的是( )A.若a垂直于α内的一条直线,则a⊥α
B.若a垂直于α内的两条直线,则a⊥α
C.若a垂直于α内的三条直线,则a⊥α
D.若a垂直于α内的两条相交直线,则a⊥α
【答案】分析:根据线面垂直的判定定理可得若a垂直于α内的两条相交直线则a⊥α,但如果没有相交的限制即使a垂直于α内的无数条直线,可不能得到线面垂直.
解答:解:若a垂直于α内的一条直线,则a与α可能平行,可能相交,也可能线在面内,故A错误
若a垂直于α内的两条平行直线,则a与α可能平行,可能相交,也可能线在面内,故B错误
若a垂直于α内的三条平行直线,则a与α可能平行,可能相交,也可能线在面内,故C错误
若a垂直于α内的两条相交直线,则由线面垂直的判定定理可得,a⊥α,故D正确
故选D
点评:本题考查的知识点是线面垂直的判定定理,熟练掌握并真正理解线面垂直判定定理的含义是解答的关键.
解答:解:若a垂直于α内的一条直线,则a与α可能平行,可能相交,也可能线在面内,故A错误
若a垂直于α内的两条平行直线,则a与α可能平行,可能相交,也可能线在面内,故B错误
若a垂直于α内的三条平行直线,则a与α可能平行,可能相交,也可能线在面内,故C错误
若a垂直于α内的两条相交直线,则由线面垂直的判定定理可得,a⊥α,故D正确
故选D
点评:本题考查的知识点是线面垂直的判定定理,熟练掌握并真正理解线面垂直判定定理的含义是解答的关键.

练习册系列答案
相关题目
 ,对
,对 都有
都有 ,则
,则 为偶函数
为偶函数 ,若对
,若对 ,都有
,都有 ,则函数
,则函数 中心对称
中心对称 与
与 是奇函数
是奇函数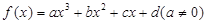 的图形一定是对称中心在图像上的中心对称图形。
的图形一定是对称中心在图像上的中心对称图形。 有两不同极值点
有两不同极值点 ,若
,若 ,且
,且 ,则关于的方程
,则关于的方程 的不同实根个数必有三个.
的不同实根个数必有三个.