题目内容
(本小题13分) 已知数列{a }满足0<a
}满足0<a , 且
, 且 (n
(n N*).
N*).
(1) 求证:an+1≠an;
(2) 令a1= ,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
【答案】
见解析。
【解析】
试题分析:(1)采用反证法,若存在正整数n使an+1=an,即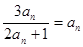 推出矛盾。
推出矛盾。
(2)运用归纳猜想的思想得到其通项公式即可。再加以证明其正确性。
解:(1) 证明:(采用反证法).若存在正整数n使an+1=an,即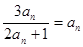 ,
解得an=0, 1.
,
解得an=0, 1.
若an=0, 则 an=an-1=…=a2=a1=0, 与题设a1>0;
若an=1, 则an=an-1=…=a2=a1=1, 与题设a1≠1相矛盾.
综上所述, an+1≠an成立.
(2) a1=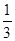 、a2=
、a2=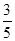 、a3=
、a3=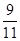 、a4=
、a4=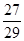 、a5=
、a5=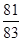 ,猜想: an=
,猜想: an=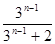 ,n∈N*.
,n∈N*.
下面用数学归纳法证明:
①n=1时, 不难验证公式成立;
②假设n=k(k∈N*)时公式成立, 即ak=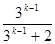
则n=k+1时, a k+1=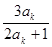 =
=
故此时公式也成立
综合① ②据数学归纳法知公式成立.
考点:本题主要考查了数列的递推关系式的运用,以及数学归纳法证明命题的运用。
点评:解决该试题的关键是利用数列的前几项得到其通项公式,然后运用数学归纳法分两步证明。

练习册系列答案
相关题目
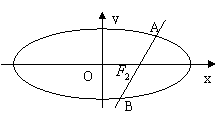
 ,实数a,b为常数),
,实数a,b为常数), 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围; 在(0,1]上解的个数。
在(0,1]上解的个数。 .
.  的最小正周期和当
的最小正周期和当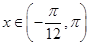 时的值域;
时的值域;
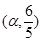 ,
,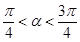 .求
.求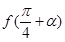 的值.
的值.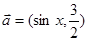 ,
,
 ∥
∥ 时,求
时,求 的值;
的值;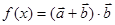 在
在 上的值域.
上的值域.