题目内容
(本题满分14分)设函数f (x)＝x3＋ax2－(2a+3)x+ a2 , a∈R．
(Ⅰ) 若x＝1是f (x)的极大值点，求实数a的取值范围；
(Ⅱ) 设函数g(x)＝bx2－(2b＋1)x＋ln x (b≠0,b∈R),若函数f (x)有极大值，且g(x)的极大值点与f (x)的极大值点相同．当
时，求证：g(x)的极小值小于－1．
满分14分。
(Ⅰ) 解: f ′(x)＝3x2＋2ax－(2a+3)＝(x－1)(3x＋2a＋3)．由于x＝1是f (x)的极大值点 ，故
，即a <－3 …………………………7分
(Ⅱ) 解: f ′(x)＝3x2＋2ax－(2a+3)＝(x－1)(3x＋2a＋3)．
g ′(x)＝
＋2bx－(2b＋1)＝
．
由于函数f (x)有极大值，故
，即
．
当 a＞－3时，即
，则f (x)的极大值点
，
所以，g(x)的极大值点
，极小值点为x＝1．
所以，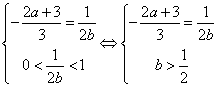
，
此时，g(x)的极小值g(1)＝b－(2b＋1)＝－1－b<－<－1．………………14分
练习册系列答案
金钥匙试卷系列答案
相关题目
，
。
，过两点
和
的中点作
轴的垂线交曲线
于点
，求证：曲线
处的切线
过点
；
，当
时
恒成立，求实数
的取值范围。
（1）求函数
的单调区间；（2）求
时，用数学归纳法证明：
的左、右焦点分别为F1与
过椭圆的一个焦点F2且与椭圆交于P、Q两点，若
的周长为
。
变成曲线
，直线
与曲线
，求
面积的取值范围。（O为坐标原点）
构成的集合：“①方
有实数根；②函数
满足
”
是集合M中的元素；
，都存在
，使得等式
成立。 
.
，求函数
的极值；
，试确定
的单调性；
，且
在
上的最大值为M，证明：
．