题目内容
已知在平面直角坐标系xOy中,向量j=(0,1),△OFP的面积为2(1)设4<t<4![]() ,求向量
,求向量![]() 与
与![]() 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设以原点O为中心,对称轴在坐标轴上,以F为右焦点的椭圆经过点M,且|![]() |=c,t=(
|=c,t=(![]() -1)c2,当|
-1)c2,当|![]() |取最小值时,求椭圆的方程.
|取最小值时,求椭圆的方程.
思路解析:此题是向量知识与圆锥曲线结合的一个问题,高考试题常用向量给出条件,运用向量知识进行转化为圆锥曲线的有关问题是常考的思想方法.设求向量![]() 与
与![]() 的夹角θ的取值范围由面积公式及
的夹角θ的取值范围由面积公式及![]() ·
·![]() =t,可求出tanθ的范围.(2)中设出P点的坐标,用c来表示|
=t,可求出tanθ的范围.(2)中设出P点的坐标,用c来表示|![]() |,求出当c取某值时的|
|,求出当c取某值时的|![]() |的最小值,进而求椭圆的方程.
|的最小值,进而求椭圆的方程.
解:(1)由2![]() =
=![]() |
|![]() |·|
|·|![]() |·sinθ,得?|
|·sinθ,得?|![]() |·|
|·|![]() |=
|=![]() ,
,
由cosθ=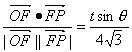 ,得tanθ=
,得tanθ=![]() .
.
∵4<t<4![]() ,∴1<tanθ<
,∴1<tanθ<![]() .
.
∵θ∈[0,π],∴夹角θ的取值范围是(![]() ,
,![]() ).
).
(2)设P(x0,y0),则![]() =(x0-c,y0),
=(x0-c,y0),![]() =(c,0).
=(c,0).
∴![]() ·
·![]() =(x0-c,y0)·(c,0)=(x0-c)c=t=(
=(x0-c,y0)·(c,0)=(x0-c)c=t=(![]() -1)c2.
-1)c2.
∴x0=![]() c.
c.
S△OFP=![]() |
|![]() |·|y0|=2
|·|y0|=2![]() ,
,
∴y0=±![]() .
.
又由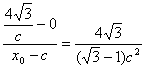 ,
,
得x0=![]() c.
c.
∴|![]() |=
|=![]() .
.
∴当且仅当![]() c=
c=![]() ,即c=2时,?|
,即c=2时,?|![]() |取最小值2
|取最小值2![]() ,
,
此时, ![]() =(2
=(2![]() ,±2
,±2![]() ),
),
∴![]() =
=![]() (2
(2![]() ,2
,2![]() )+(0,1)=(2,3)或
)+(0,1)=(2,3)或![]() =
=![]() (2
(2![]() ,-2
,-2![]() )+(0,1)=(2,-1).
)+(0,1)=(2,-1).
椭圆长轴2a=![]() =8,
=8,
∴a=4,b2=12或2a=![]() .
.
∴a=![]() ,b2=
,b2=![]() .
.
故所求椭圆方程为![]() =1或
=1或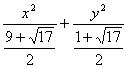 =1.
=1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目