题目内容
已知三次函数f(x)的最高次项系数为a,三个零点分别为-1,0,3.(1)若方程
 有两个相等的实根,求a的值;
有两个相等的实根,求a的值;(2)若函数λ(x)=f(x)+2x2在区间
 内单调递减,求a的取值范围.
内单调递减,求a的取值范围.
【答案】分析:(1)根据函数模型可设出函数解析式,代入方程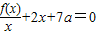 ,然后根据方程有两个相等的实根,利用判别式为0建立等式关系,解之即可.
,然后根据方程有两个相等的实根,利用判别式为0建立等式关系,解之即可.
(2)λ(x)在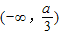 内单调递减,可转化成λ'(x)≤0在
内单调递减,可转化成λ'(x)≤0在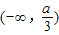 恒成立,然后讨论a,建立关于a的不等关系,解之即可.
恒成立,然后讨论a,建立关于a的不等关系,解之即可.
解答:解:(1)依题意,设f(x)=ax(x+1)(x-3)
∵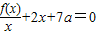 有两个相等实根,
有两个相等实根,
即ax2-(2a-2)x+4a=0有两个相等实根,
∴△=(2a-2)2-4a•4a=0,
即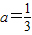 或a=-1.
或a=-1.
(2)∵λ(x)=ax3-(2a-2)x2-3ax在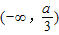 内单调递减,
内单调递减,
∴λ'(x)=3ax2-2(2a-2)x-3a≤0在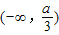 恒成立,
恒成立,
∴a=0或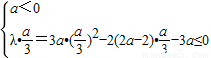
解得a=0或a≤-1
点评:本题主要考查了函数的单调性与导数的关系,以及恒成立问题,同时考查了等价转化的思想和运算求解的能力,属于基础题.
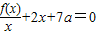 ,然后根据方程有两个相等的实根,利用判别式为0建立等式关系,解之即可.
,然后根据方程有两个相等的实根,利用判别式为0建立等式关系,解之即可.(2)λ(x)在
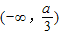 内单调递减,可转化成λ'(x)≤0在
内单调递减,可转化成λ'(x)≤0在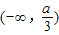 恒成立,然后讨论a,建立关于a的不等关系,解之即可.
恒成立,然后讨论a,建立关于a的不等关系,解之即可.解答:解:(1)依题意,设f(x)=ax(x+1)(x-3)
∵
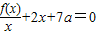 有两个相等实根,
有两个相等实根,即ax2-(2a-2)x+4a=0有两个相等实根,
∴△=(2a-2)2-4a•4a=0,
即
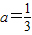 或a=-1.
或a=-1.(2)∵λ(x)=ax3-(2a-2)x2-3ax在
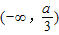 内单调递减,
内单调递减,∴λ'(x)=3ax2-2(2a-2)x-3a≤0在
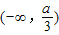 恒成立,
恒成立,∴a=0或
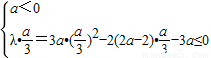
解得a=0或a≤-1
点评:本题主要考查了函数的单调性与导数的关系,以及恒成立问题,同时考查了等价转化的思想和运算求解的能力,属于基础题.

练习册系列答案
相关题目
 已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则
已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则