题目内容
如图,正四棱柱AC1中,对角线BD1=8,BD1与侧面BC1所成的角为30°,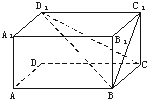
求:(1)BD1和底面ABCD所成的角;
(2)异面直线BD1和AD所成的角;
(3)正四棱柱的全面积.
答案:
解析:
解析:
| 解:(1)由于正四棱柱是长方体,D1C1⊥面BC1,
∴∠D1BC1是BD1与侧面BC1所成的角.∴∠D1BC1=30°. ∵BD1=8,∴C1D1=4.∴BD=4 ∵DD1⊥底面ABCD,∴BD1和底面ABCD所成的角就是∠D1BD. 在Rt△D1BD中,cosD1BD= ∴BD1和底面ABCD所成的角是45°. (2)∵AD∥BC, ∴∠D1BC(或其补角)是异面直线BD1和AD所成的角.连结D1C, 在Rt△D1BC中,cosD1BC= ∴异面直线BD1和AD所成的角是60°. (3)在Rt△D1BC1中,BC1=BD1cosD1BC1=8cos30°=4 ∴CC1=4 ∴S全=S侧+2S底=64
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
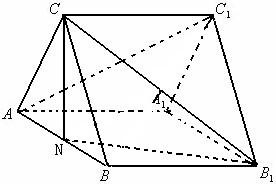 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.

