Question

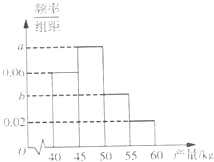（2013•广州一模）沙糖桔是柑桔类的名优品种，因其味甜如砂糖故名，某果农选取一片山地种植沙糖桔，收获时，该果农随机选取果树20株作为样本测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]，进行分组，得到频率分布直方图如图3，已知样本中产量在区间（45，50]上的果树株数是产量在区间（50，60]上的果树株数的

4

3

倍．
（1）求a，b的值；
（2）从样本中产量在区间（50，60]上的果树随机抽取两株，求产量在区间（55，60]上的果树至少有一株被抽中的概率．

Answer 1

分析：（1）根据频率的求法及所有小组的频率和为1，由已知得：

a= 4 3 (b+0.02) (0.06+a+b+0.02)×5=1

，解之即得a，b的值；
（2）根据概率的求法，计算可得答案，分别求出包含基本事件及从（50，60]中任意抽取2个个体基本事件总数，最后求出它们的比值即可．

解答：解：（1）由题意知：

a= 4 3 (b+0.02) (0.06+a+b+0.02)×5=1

解得：

a=0.08 b=0.04

，（4分）
（2）在（50，55]中有4个个体，在（55，60]中有2个个体，所以（50，60]中共6个个体．
所以从（50，60]中任意抽取2个个体基本事件总数为

C

2 6

=15个，（8分）
设“至少有一个个体落在（55，60]之间”为事件A，
则A包含基本事件15-C

2 4

=9个，（10分）
所以P（A）=

9

15

=

3

5

．（12分）

点评：本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．