题目内容
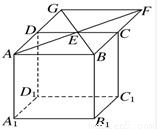
在正方体AC1中,E、F分别是相邻两个侧面BCC1B1和CDD(1)试判断直线A1E与B
(2)求直线A1E与直线B
(3)求直线A1E与平面B1CD1所成的角.
解:如图,(1)连结CD1、CB1、B1D1,依题意,E、F分别是CD1与CB1的中点,由于A1![]() 平面B1CD1,E
平面B1CD1,E![]() 平面B1CD1,B
平面B1CD1,B![]() 平面B1CD1,且E
平面B1CD1,且E![]() B
B
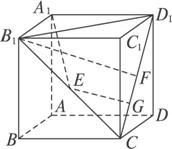
∴直线A1E与B
(2)取CF的中点G,连结EG,则EG∥B
∴A1E与FG所成的不大于90°的正角即为异面直线A1E与B![]() ,
,
EG2=![]() B
B![]() (
(![]() )2=
)2=![]() a2,A
a2,A![]() a2,
a2,
∴cos∠A1EG=![]() ,
,
故所求的角为arccos![]() .
.
(3)连结A
∵B1D1⊥A
∴B1D1⊥平面CC
∴平面B1CD1⊥平面CC
连结CO1,则CO1为平面B1CD1与平面CC
又A![]() ,
,
![]() ,
,
在Rt△A1EM中,sin∠A1EM=![]() .
.
∴直线A1E与平面B1CD1所成的角为arcsin![]() .
.

练习册系列答案
相关题目
在正方体AC1中,E、F分别为AB和CD的中点,则异面直线A1E与BF所成角的余弦值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
 在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG.
在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG.