题目内容
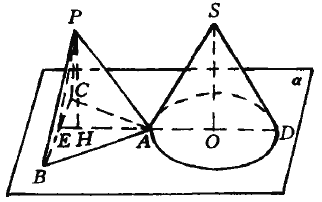
【题目】如图,三棱锥![]() 的底面
的底面![]() 与圆锥
与圆锥![]() 的底面
的底面![]() 都在平面
都在平面![]() 上,且
上,且![]() 过点
过点![]() ,又
,又![]() 的直径
的直径![]() ,垂足为
,垂足为![]() .设三棱锥
.设三棱锥![]() 的所有棱长都是1,圆锥的底面直径与母线长也都是1,圆锥的底面直径与母线长也都是1.求圆锥的顶点
的所有棱长都是1,圆锥的底面直径与母线长也都是1,圆锥的底面直径与母线长也都是1.求圆锥的顶点![]() 到三棱锥
到三棱锥![]() 的三个侧面的距离.
的三个侧面的距离.
【答案】S到侧面![]() 的距离与S到侧面
的距离与S到侧面![]() 的距离都是
的距离都是![]() ,S到侧面
,S到侧面![]() 的距离
的距离![]()
【解析】
先求S到侧面![]() 的距离.
的距离.
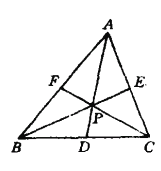
设![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() .作
.作![]() ,垂足为
,垂足为![]() ,则
,则![]() .可知
.可知![]() 在同一平面
在同一平面![]() 上.设
上.设![]() 与
与![]() 的交点为
的交点为![]() (如图).
(如图).
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 的长度即为
的长度即为![]() 到侧面
到侧面![]() 的距离.
的距离.

易知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
由![]() ,得
,得![]() .
.
∴![]() ,
,![]()
由![]() ,得
,得![]() .
.
再求S到侧面![]() 的距离.
的距离.

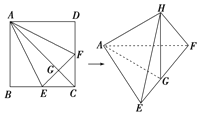
连结![]() 交
交![]() 于
于![]() ,并延长到
,并延长到![]() ,使
,使![]() (如上左图).过
(如上左图).过![]() 作
作![]() 平面
平面![]() ,且取
,且取![]() ,
,![]() 与
与![]() 均在
均在![]() 的同一侧.连结
的同一侧.连结![]() ,则
,则![]() ,
,![]() 面
面![]() ,
,![]() 在平面
在平面![]() 内.连结
内.连结![]() ,则
,则![]() .作
.作![]() ,垂足为K(如上右图),则
,垂足为K(如上右图),则![]() 的长度为S到侧面
的长度为S到侧面![]() 的距离.
的距离.
易知![]() .记
.记![]() ,则
,则![]() .
.
从而,![]() .
.
∴![]() .
.
又![]() .
.
在![]() 中,
中,![]()
由对称性知,S到侧面![]() 的距离也是
的距离也是![]() .
.

练习册系列答案
相关题目