题目内容
(14 分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率
分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率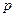 与每日生产产品件数
与每日生产产品件数 (
(
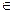
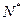 )间的关系为
)间的关系为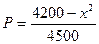 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
(Ⅰ)将日利润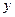 (元)表示成日产量
(元)表示成日产量 (件)的函数;
(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值
解:(I)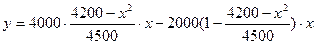 .………………4分
.………………4分
=3600 -
-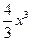
∴所求的函数关系是y=-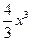 +3600
+3600 (
(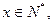 1≤x≤40).………
1≤x≤40).……… ………6分
………6分
(II)显然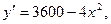 令y′=0,解得x=30.
令y′=0,解得x=30.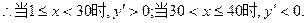
∴函数y=-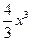 +3600x(x∈N*,1≤x≤40)在
+3600x(x∈N*,1≤x≤40)在 上是单调递增函数,
上是单调递增函数,
在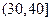 上是单调递减函数. …………………………10分
上是单调递减函数. …………………………10分
∴当x=30时,函数y=-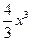 +3600x(x∈N*,1≤
+3600x(x∈N*,1≤ x≤40)取最大值,最大值为
x≤40)取最大值,最大值为
-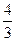 ×303+3600×30=72000(元).
×303+3600×30=72000(元).
∴该厂的日产量为30件时,日利润最大,其最大值为72000元.…………14分
解析

练习册系列答案
相关题目
由直线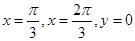 与曲线
与曲线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
| A.1 | B. | C. | D.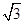 |
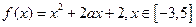 .
. 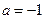 时,求函数f(x)
时,求函数f(x) 的最大值和最小值;
的最大值和最小值;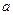 的取值范围,使
的取值范围,使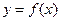 在区间
在区间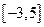 上是单调函数
上是单调函数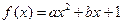 (
(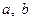 为实数,
为实数,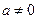 ,
,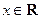 ),
),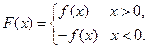
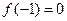 ,且函数
,且函数 的值域为
的值域为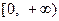 ,求
,求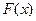 的表达式;
的表达式; 时,
时,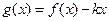 是单调函数,求实数
是单调函数,求实数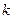 的取值范围;
的取值范围;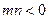 ,
,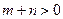 ,
,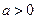 ,且函数
,且函数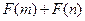 是否大于
是否大于 ?
? 的图像经过坐
的图像经过坐 标原
标原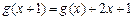 ,设函数
,设函数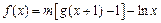 ,其中m为常数且
,其中m为常数且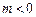 。
。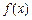 的单调性并说明理由。
的单调性并说明理由。 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0). 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;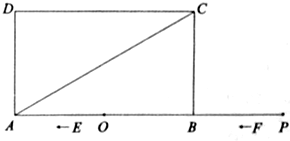
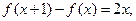 且f(0)=1.
且f(0)=1. 上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围. 的图象与x轴有两个不同的公共点,且
的图象与x轴有两个不同的公共点,且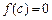 ,当
,当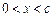 时,恒有
时,恒有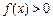 .
.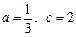 时,求不等式
时,求不等式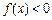 的解集;
的解集;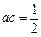 ,求a的值;
,求a的值;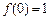 ,且
,且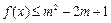 对所有
对所有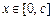 恒成立,求正实数m的最小值.
恒成立,求正实数m的最小值.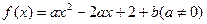 ,在区间
,在区间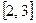 上有最大值5,最小
上有最大值5,最小 上单调,求
上单调,求 的取值范围。
的取值范围。