题目内容
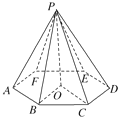 如图所示,已知六棱锥P-ABCDEF,其中底面ABCDEF是正六边形,点P在底面的投影是正六边形的中心,底面边长为2cm,侧棱长为3cm,求六棱锥P-ABCDEF的表面积和体积.
如图所示,已知六棱锥P-ABCDEF,其中底面ABCDEF是正六边形,点P在底面的投影是正六边形的中心,底面边长为2cm,侧棱长为3cm,求六棱锥P-ABCDEF的表面积和体积.分析:根据题意,过O作边AB的垂线,垂足为Q,连结PQ,则可得六棱锥的斜高PQ,通过正六棱锥的侧棱,求出棱锥的高,即可求出正六棱锥的表面积与体积.
解答: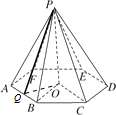 解:P-ABCDEF为正六棱锥,O是底面正六边形ABCDEF的中心.
解:P-ABCDEF为正六棱锥,O是底面正六边形ABCDEF的中心.
连接OA、OB、OP,过O作边AB的垂线,垂足为Q.连结PQ,
∵ABCDEF为正六边形,∴△AOB为等边三角形.
∴OA=OB=AB=2,又∵OQ⊥AB,∴Q是AB中点.
∴AQ=BQ=1,侧棱长为3cm,
∴斜高PQ=
=2
,
∵OP⊥面ABCDEF,
∴OP是棱锥的高,PO=
=
.
∴该棱锥的表面积为:S=S底+S侧=6×
×22+6×
×2×2
=6
+12
.
正六棱锥的体积为V=
×6
×
=2
.
 解:P-ABCDEF为正六棱锥,O是底面正六边形ABCDEF的中心.
解:P-ABCDEF为正六棱锥,O是底面正六边形ABCDEF的中心.连接OA、OB、OP,过O作边AB的垂线,垂足为Q.连结PQ,
∵ABCDEF为正六边形,∴△AOB为等边三角形.
∴OA=OB=AB=2,又∵OQ⊥AB,∴Q是AB中点.
∴AQ=BQ=1,侧棱长为3cm,
∴斜高PQ=
| 32-12 |
| 2 |
∵OP⊥面ABCDEF,
∴OP是棱锥的高,PO=
| 32-22 |
| 5 |
∴该棱锥的表面积为:S=S底+S侧=6×
| ||
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
正六棱锥的体积为V=
| 1 |
| 3 |
| 3 |
| 5 |
| 15 |
点评:本题以正六棱锥为载体,考查棱锥的底面积,侧面积与体积的关系,考查计算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目


 的底面是正六边形,
的底面是正六边形, 平面
平面 ,
, 是
是 的中点。
的中点。
 //平面
//平面 ;
; ,当二面角
,当二面角 的大小为
的大小为 时,求
时,求 的值。
的值。 ,M是PA的中点.
,M是PA的中点.