题目内容
已知 且
且 ,函数
,函数 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
C
解析试题分析:当 时,指数函数和对数函数均递增,且直线
时,指数函数和对数函数均递增,且直线 和
和 轴交点在
轴交点在 的上方,故可排除A,B;当
的上方,故可排除A,B;当 时,指数函数和对数函数均递减,且直线
时,指数函数和对数函数均递减,且直线 和
和 轴交点在
轴交点在 的下方,故选C.
的下方,故选C.
考点:指数函数、对数函数、一次函数的图像和性质.

练习册系列答案
相关题目
 的零点个数为( )
的零点个数为( )
| A.4 | B.5 | C.6 | D.7 |
设偶函数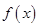 满足
满足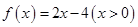 ,则不等式
,则不等式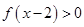 的解集为( )
的解集为( )
A.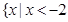 或 或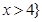 | B.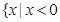 或 或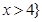 | C.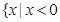 或 或 | D.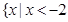 或 或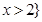 |
映射f:X→Y是定义域到值域的函数,则下面四个结论中正确的是( )
| A.Y中的元素不一定有原象 |
| B.X中不同的元素在Y中有不同的象 |
| C.Y可以是空集 |
| D.以上结论都不对 |
偶函数 在区间[0,4]上单调递减,则有( )
在区间[0,4]上单调递减,则有( )
A. |
B. |
C. |
D. |
设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
定义在 上的函数
上的函数 满足
满足 则
则 的值为( )
的值为( )
A. | B. | C. | D. |
已知 是函数
是函数 的零点,若
的零点,若 ,则
,则 的值满足( )
的值满足( )
A. | B. |
C. | D. 的符号不确定 的符号不确定 |
 的图象的大致形状是
的图象的大致形状是