题目内容
若函数 f（x）=2x+1nx，，且f′（a）=0，则2a1n2a=（ ）A．l
B．-1
C．-ln2
D．ln2
【答案】分析：求导数代值可得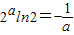
，而要求的式子由对数的运算性质可化为2aln2×a，代值可得答案．
解答：解：∵函数 f（x）=2x+1nx，∴f′（x）=2xln2+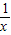
，
由已知f′（a）=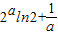
=0，即
，
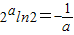故2aln2a=2a×aln2=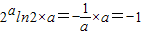
，
故选B
点评：本题考查导数的运算以及对数函数的性质，属基础题．
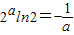，而要求的式子由对数的运算性质可化为2aln2×a，代值可得答案．解答：解：∵函数 f（x）=2x+1nx，∴f′（x）=2xln2+
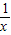，由已知f′（a）=
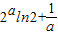=0，即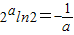，故2aln2a=2a×aln2=
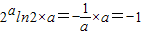，故选B
点评：本题考查导数的运算以及对数函数的性质，属基础题．
练习册系列答案
相关题目
若函数f（x）=2-|x|-x2+a有两个不同的零点，则实数a的取值范围是（ ）
| A、[1，+∞） | B、（1，+∞） | C、[-1，+∞） | D、（-1，+∞） |