题目内容
已知:函数g(x)=ax2-2ax+1+b(a≠0,b<1),在区间 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数 .
.(1)求a、b的值及函数f(x)的解析式;
(2)若不等式f(2x)-k•2x≥0在
 时恒成立,求实数k的取值范围.
时恒成立,求实数k的取值范围.
【答案】分析:(1)由二次函数g(x)=ax2-2ax+1+b的对称轴为x=1,由题意得 ,或
,或  ,解得a、b的值,即可得到函数f(x)的解析式.
,解得a、b的值,即可得到函数f(x)的解析式.
(2)不等式即 ,在
,在 时,设
时,设 ,则k≤(t-1)2,
,则k≤(t-1)2,
根据(t-1)2min>0,求得实数k的取值范围.
解答:解:(1)由于二次函数g(x)=ax2-2ax+1+b的对称轴为x=1,
由题意得:1° ,解得
,解得 .
.
或 2° ,解得
,解得 .(舍去)
.(舍去)
∴a=1,b=0…(6分)
故g(x)=x2-2x+1, . …(7分)
. …(7分)
(2)不等式f(2x)-k•2x≥0,即 ,∴
,∴ .…(10分)
.…(10分)
在 时,设
时,设 ,∴k≤(t-1)2,
,∴k≤(t-1)2,
由题意可得,函数f(x)的定义域为{x|x≠0},故t≠1,即 ≤t≤2,且t≠1.
≤t≤2,且t≠1.
∵(t-1)2min>0,∴k≤0,即实数k的取值范围为(-∞,0].…(14分)
点评:本题主要考查求二次函数在闭区间上的最值,用待定系数法求函数的解析式,函数的恒成立问题,属于中档题.
 ,或
,或  ,解得a、b的值,即可得到函数f(x)的解析式.
,解得a、b的值,即可得到函数f(x)的解析式.(2)不等式即
 ,在
,在 时,设
时,设 ,则k≤(t-1)2,
,则k≤(t-1)2,根据(t-1)2min>0,求得实数k的取值范围.
解答:解:(1)由于二次函数g(x)=ax2-2ax+1+b的对称轴为x=1,
由题意得:1°
 ,解得
,解得 .
.或 2°
 ,解得
,解得 .(舍去)
.(舍去) ∴a=1,b=0…(6分)
故g(x)=x2-2x+1,
 . …(7分)
. …(7分)(2)不等式f(2x)-k•2x≥0,即
 ,∴
,∴ .…(10分)
.…(10分)在
 时,设
时,设 ,∴k≤(t-1)2,
,∴k≤(t-1)2,由题意可得,函数f(x)的定义域为{x|x≠0},故t≠1,即
 ≤t≤2,且t≠1.
≤t≤2,且t≠1.∵(t-1)2min>0,∴k≤0,即实数k的取值范围为(-∞,0].…(14分)
点评:本题主要考查求二次函数在闭区间上的最值,用待定系数法求函数的解析式,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
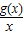 .
.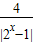 -3)=0有三个相异的实数根,求实数t的取值范围.
-3)=0有三个相异的实数根,求实数t的取值范围. .
. -3)=0有三个相异的实数根,求实数t的取值范围.
-3)=0有三个相异的实数根,求实数t的取值范围.