题目内容
已知3sinα=sin(α+2β),求证:tan(α+β)=2tanβ.
答案:
解析:
解析:
|
思路分析:观察条件等式和结论等式中的角,条件中含有β、2α+β,结论中含有α+β、α,若从条件入手,可采用角的变换,α=(α+β)-β,2α+β=(α+β)+β,展开后转化成齐次整式,约分得出结论. 证明:∵3sinα=3sin[(α+β)-β] =3sin(α+β)cosβ-3cos(α+β)sinβ, sin(α+2β)=sin[(α+β)+β] =sin(α+β)cosβ+cos(α+β)sinβ, 又3sinα=sin(α+2β), ∴3sin(α+β)cosβ-3cos(α+β)sinβ=sin(α+β)cosβ+cos(α+β)sinβ. ∴2sin(α+β)cosβ=4cos(α+β)sinβ. ∴tan(α+β)=2tanβ. 方法归纳:对条件恒等式的证明,若条件复杂,可从化简条件入手得出结论;若结论复杂,可化简结论;若条件和结论都较为复杂,可同时化简它们,直到找到它们间的联系. 深化升华:三角恒等式的证明实质就是由一种结构形式转化为另一种结构形式.因此证明恒等式的基本思路是:证明等式时必须仔细观察等式两边结构上的差异,然后分析这些差异和联系,最后从解决差异入手,施行适当的变换,直至消除这些差异完成恒等式的证明. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
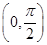 ,若a∥b,则tan
,若a∥b,则tan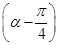 =( )
=( )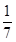 B.-
B.-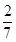 D.-
D.- =(sin
=(sin ,1),
,1), =(1,cos
=(1,cos .
.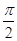 ),则sinx=______________.
),则sinx=______________. =(sin
=(sin ,1),
,1), =(1,cos
=(1,cos .
.