题目内容
设F(1,0),M点在x轴上,P点在y轴上,且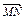 =2
=2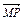 ,
,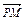 ⊥
⊥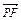 ,当点P
,当点P
在y轴上运动时,求点N的轨迹方程.
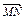 =2
=2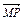 ,
,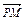 ⊥
⊥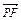 ,当点P
,当点P在y轴上运动时,求点N的轨迹方程.
y2=4x
设M(x0,0),P(0,y0),N(x,y),
由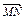 =2
=2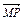 得(x-x0,y)=2(-x0,y0),
得(x-x0,y)=2(-x0,y0),
∴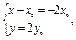 即
即
∵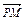 ⊥
⊥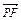 ,
,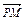 =(x0,-y0),
=(x0,-y0), 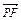 =(1,-y0),
=(1,-y0),
∴(x0,-y0)·(1,-y0)=0,∴x0+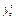 =0.
=0.
∴-x+ =0,即y2=4x.故所求的点N的轨迹方程是y2=4x.
=0,即y2=4x.故所求的点N的轨迹方程是y2=4x.
由
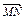 =2
=2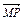 得(x-x0,y)=2(-x0,y0),
得(x-x0,y)=2(-x0,y0),∴
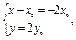 即
即
∵
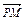 ⊥
⊥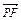 ,
,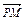 =(x0,-y0),
=(x0,-y0), 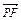 =(1,-y0),
=(1,-y0),∴(x0,-y0)·(1,-y0)=0,∴x0+
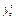 =0.
=0.∴-x+
 =0,即y2=4x.故所求的点N的轨迹方程是y2=4x.
=0,即y2=4x.故所求的点N的轨迹方程是y2=4x.
练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
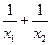
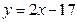 上,另外两个顶点在抛物线
上,另外两个顶点在抛物线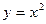 上.则该正方形面积的最小值为 .
上.则该正方形面积的最小值为 .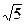 .
.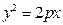 上有三点
上有三点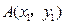 ,
,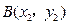 ,
,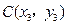 且
且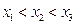 ,若线段
,若线段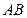 ,
,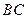 在
在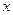 轴上射影之长相等,求证:
轴上射影之长相等,求证: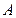 ,
,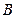 ,
,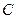 三点到焦点的距离顺次成等差数列.
三点到焦点的距离顺次成等差数列.
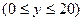 ,
,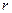 的范围为 ( )
的范围为 ( )
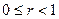

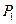 ,
,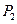 ,…,
,…,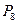 是抛物线
是抛物线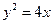 上的点,它们的横坐标依次为
上的点,它们的横坐标依次为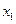 ,
,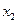 ,…,
,…,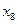 ,F是抛物线的焦点,若
,F是抛物线的焦点,若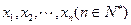 成等差数列且
成等差数列且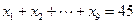 ,则
,则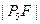 =( ).
=( ).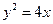
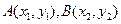
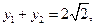
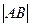
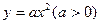 的焦点F作一直线交抛物线于P、Q两点,若线段DF与FQ的长分别是p,q,则
的焦点F作一直线交抛物线于P、Q两点,若线段DF与FQ的长分别是p,q,则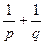 等于______________。
等于______________。