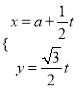题目内容
【题目】(本小题共12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=![]() AD=1,CD=
AD=1,CD=![]() .
.
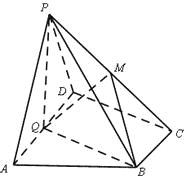
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
【答案】(1)∵AD //BC,BC=![]() AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD// BQ.∵∠ADC=90°∴∠AQB=90°即QB⊥AD.又∵平面PAD⊥平面ABCD 且平面PAD∩平面ABCD=AD,∴BQ⊥平面PAD.∵BQ
AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD// BQ.∵∠ADC=90°∴∠AQB=90°即QB⊥AD.又∵平面PAD⊥平面ABCD 且平面PAD∩平面ABCD=AD,∴BQ⊥平面PAD.∵BQ![]() 平面PQB,∴平面PQB⊥平面PAD.
平面PQB,∴平面PQB⊥平面PAD.
(2)![]() .
.
【解析】试题分析:(1)∵AD //BC,BC=![]() AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD// BQ.∵∠ADC=90°∴∠AQB=90°即QB⊥AD.
AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD// BQ.∵∠ADC=90°∴∠AQB=90°即QB⊥AD.
又∵平面PAD⊥平面ABCD 且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ![]() 平面PQB,∴平面PQB⊥平面PAD.
平面PQB,∴平面PQB⊥平面PAD.
(2)∵PA=PD,Q为AD的中点, ∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为![]() ;
;![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,
∴ , ∴
, ∴
在平面MBQ中,![]() ,
,![]() ,
,
∴ 平面MBQ法向量为![]() .
.
∵二面角M-BQ-C为30,![]()
∴![]() .
.

练习册系列答案
相关题目