题目内容
已知函数f（x）在定义域 （-∞，0）∪（0，+∞）上是奇函数，且当x＞0时，函数f（x）的表达式为f（x）=x2+lnx，则当x＜0时，函数f（x）的表达式是（ ）
分析：根据x＞0时，f（x）=x2+lnx，由x＜0时，-x＞0，代入可得f（-x）的表达式，进而根据函数f（x）是定义在 （-∞，0）∪（0，+∞）上是奇函数，由f（x）=-f（-x）可得答案．
解答：解：当x＜0时，-x＞0时，
∵当x＞0时，f（x）=x2+lnx，
∴f（-x）=（-x）2+ln（-x）=x2+ln（-x），
又∵函数f（x）在定义域 （-∞，0）∪（0，+∞）上是奇函数，
∴f（x）=-f（-x）=-x2-ln（-x），
故选A
∵当x＞0时，f（x）=x2+lnx，
∴f（-x）=（-x）2+ln（-x）=x2+ln（-x），
又∵函数f（x）在定义域 （-∞，0）∪（0，+∞）上是奇函数，
∴f（x）=-f（-x）=-x2-ln（-x），
故选A
点评：本题考查的知识点是函数解析式的求法，函数的奇偶性，熟练掌握奇函数在对称区间上解析式的求解方法和步骤是解答的关键．
练习册系列答案
相关题目
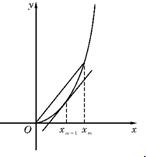已知函数f（x）=x3+x2，数列|xn|（xn＞0）的第一项xn=1，以后各项按如下方式取定：曲线x=f（x）在（xn+1，f（xn+1））处的切线与经过（0，0）和（xn，f （xn））两点的直线平行（如图）．
中ξi的选取是任意的，且In仅于n有关．